Линейные ДУ 2-го порядка с постоянными коэффициентами. Метод вариации произвольных постоянных решения ДУ.

Общий вид: 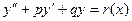(11) Здесь 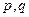- константы, 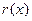- функция. При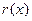 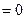уравнение 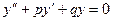(12) называется однородным, иначе – неоднородным.

Существует единственное решение уравнения (11). Удовлетворяющее начальным условиям: 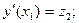где 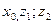- числа.

Линейной комбинацией функций и 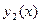называется выражение вида 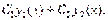где С₁, С₂ – произвольные коэффициенты.

Функция и 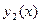называются линейно независимыми, если их линейная комбинация равна нулевой функции только в случае С₁=С₂=0, в противном случае функция 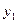и называются линейно зависимыми.

Рассмотрим решение однородного уравнения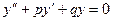

Все решения здесь обладают структурой линейного пространства: если 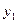, - решения (12), то и их линейная комбинация – тоже решение этого уравнения. Чтобы доказать это, достаточно подставить эту линейную комбинацию в уравнение (12).

Теорема. Если и 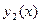- линейно независимые частные решения уравнения (12), то общее решение этого уравнения является линейной комбинацией этих частных решений.

Будем искать решение уравнения (12) в форме 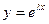, где - некоторое действительное число. Подставим в, получим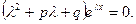

Функция (13) является решением (12). Если есть корень уравнения:

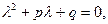которое называется характеристическим уравнением исходного уравнения

Теорема. Пусть уравнение (14) имеет действительные корни 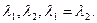Тогда общее решение (12) имеет вид: 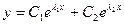, где С₁, С₂ – некоторые числа;

Если уравнение имеет кратный корень 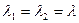, то общее решение имеет вид:

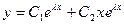, где С₁, С₂ –некоторые числа;

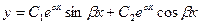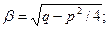
Если уравнение не имеет действительных корней, то общее решение имеет вид: , где - некоторые числа.

Пример. Найти частное решение уравнения 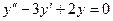при начальных условиях 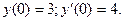Решаем характеристическое уравнение 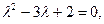находим корни

Общее решение имеет вид:

Найдём такие значения констант, при которых выполняются заданные начальные условия: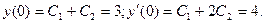

Решаем систему: ; получаем С₁=2; С₂=1. Отсюда

Неоднородное уравнение (11) может быть решено методом вариации произвольных постоянных. Сначала находится общее решение 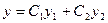уравнения (12), имеющего ту же левую часть, что и исходное уравнение (11). Затем решение уравнения (11) находится в виде 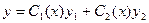, т.е. предполагается, что С₁ и С₂ являются функциями независимой переменной х. При этом функции С₁(х) и С₂(х) могут быть найдены из решения системы

16) Числовой ряд, его сходимость и сумма. Необходимый признак сходимости. Свойства сходящихся рядов. Геометрический и обобщенный гармонический ряды.

Дата добавления: 2015-08-21