Распространение сигнала от источника для случая цилидрических волн.

Рассмотрим теперь цидиндрический () случай, т. е. случай волн симметричных относительно оси координат , здесь - расстояние от оси симметрии (Рис 4.1).

Рис. 4.1

В этом случае волновое уравнение (1.29.2) примет вид:

, (4.1)

Построение решения уравнения (4.1) будет основываться на обобщении найденного выше (формула (3.24)) решения для сферически-симметричного случая для источника, генерирующего только уходящие волны. Для этого положим, что источники распределены равномерно вдоль оси с плотностью на единицу длины (Рис. 4.1). В этом случае полное возмущение, создаваемое таким распределением, является функцией только от расстояния до оси и от времени . Таким образом, мы получаем цилиндрическую волну, генерируемую линейным источником. Полное возмущение, следуя (3.24), тогда будет равно

, где (4.2)

Полученное решение (4.2) может быть записано в различных формах. Так, подставив в интеграл , получим

(4.3)

Применив другую подстановку , , получим

(4.4)

Формула (4.3) удобнее для вычисления производных от и, следовательно, для непосредственной проверки справедливости волнового уравнения для полученного решения в форме (4.3). Действительно, после вычисления соотв. производных и подстановки в (4.1) получим, что

Последний предел равен нулю, если, например, , или, например, если , что завершает проверку.

Из формулы (4.4) в отличие от плоского случая (3.5) или сферического (3.24) не следует, что возмущение от источника, издававшего сигнал в течение промежутка времени Т, ограничено во времени интервалом

Т. е., если принять, что источник издавал сигнал в течение промежутка времени , то в цилиндрическом случае первый сигнал к наблюдателю прибывает с волновым фронтом, покинувшим источник при , но действие возмущения продолжается и после момента времени . Действительно, из представления решения (4.4) имеем:

, где .

Тогда для фиксированного получим оценку

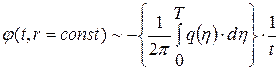при , т.е. возмущение будет стремится к нулю только асимптотически при .

Это важное различие между нечетным и четным числом измерений было замечено Адамаром. Можно сказать, что иметь дело с нечетным числом измерений проще, чем с четным, поэтому цилиндрическое волновое решение было выведено из сферического волнового решения. Другим способом получить указанное решение можно было методом спуска из общего решения Пуассона для трехмерного случая.

Дата добавления: 2015-10-23