
|
Читайте также: |
Для данной задачи (см Приложение 5) составить форму ввода (или загрузить из файла, подготовленного преподавателем), ввести исходные данные и зависимости из математической модели. Вызвать диалоговое окно Поиск решения, ввести адрес целевой функции, указать изменяемые ячейки, ввести ограничения и граничные условия. В диалоговом окне Параметры установить флажок Линейная модель. Запустить алгоритм поиска оптимального решения. По полученным результатам сформулировать вывод
Приложения
Приложение 1. Численное интегрирование. Варианты самостоятельных работ
№ 1 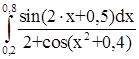 № 2
№ 2 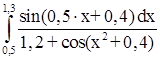 № 3
№ 3 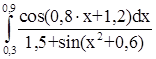
№ 4 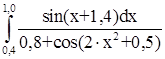 № 5
№ 5 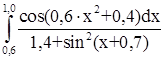 № 6
№ 6 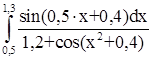
№ 7 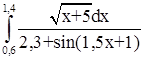 № 8
№ 8 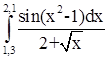 № 9
№ 9 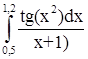
№ 10 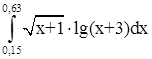 № 11
№ 11 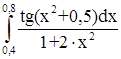 № 12
№ 12 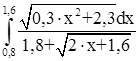
Приложение 2. Численное интерполирование. Варианты самостоятельных работ
| Вариант 1 | ||||||
| Задача 1 | ||||||
| x | -1 | |||||
| y | -3 | |||||
| Задача 2 | ||||||
| x | 0,43 | 0,48 | 0,55 | 0,62 | 0,7 | 0,75 |
| y | 1,63597 | 1,73234 | 1,87686 | 2,03345 | 2,22846 | 2,35973 |
| arg=0,702 | ||||||
| Вариант 2 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | ||||||
| Задача 2 | ||||||
| x | 0,02 | 0,08 | 0,12 | 0,17 | 0,23 | 0,3 |
| y | 1,02316 | 1,0959 | 1,14725 | 1,21483 | 1,3012 | 1,40976 |
| arg=0,102 | ||||||
| Вариант 3 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -1 | -4 | ||||
| Задача 2 | ||||||
| x | 0,35 | 0,41 | 0,47 | 0,51 | 0,56 | 0,64 |
| y | 2,73951 | 2,3008 | 1,96864 | 1,78776 | 1,59502 | 1,3431 |
| arg=0,526 | ||||||
| Вариант 4 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -2 | |||||
| Задача 2 | ||||||
| x | 0,41 | 0,46 | 0,52 | 0,6 | 0,65 | 0,72 |
| y | 2,57418 | 2,32513 | 2,09336 | 1,86203 | 1,74926 | 1,62098 |
| arg=0,616 | ||||||
| Вариант 5 | ||||||
| Задача 1 | ||||||
| x | -3 | -1 | ||||
| y | -1 | |||||
| Задача 2 | ||||||
| x | 0,68 | 0,73 | 0,8 | 0,88 | 0,93 | 0,99 |
| y | 0,80866 | 0,89492 | 1,02964 | 1,20966 | 1,34087 | 1,52368 |
| arg=0,896 |
| Вариант 6 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -3 | -7 | ||||
| Задача 2 | ||||||
| x | 0,11 | 0,15 | 0,21 | 0,29 | 0,35 | 0,4 |
| y | 9,05421 | 6,61659 | 4,6917 | 3,35106 | 2,73951 | 2,36522 |
| arg=0,314 | ||||||
| Вариант 7 | ||||||
| Задача 1 | ||||||
| x | -2 | -1 | ||||
| y | ||||||
| Задача 2 | ||||||
| x | 0,43 | 0,48 | 0,55 | 0,62 | 0,7 | 0,75 |
| y | 1,63597 | 1,73234 | 1,87686 | 2,03345 | 2,22846 | 2,35973 |
| arg=0,512 | ||||||
| Вариант 8 | ||||||
| Задача 1 | ||||||
| X | ||||||
| Y | -3 | |||||
| Задача 2 | ||||||
| x | 0,02 | 0,08 | 0,12 | 0,17 | 0,23 | 0,3 |
| y | 1,02316 | 1,0959 | 1,14725 | 1,21483 | 1,3012 | 1,40976 |
| arg=0,114 | ||||||
| Вариант 9 | ||||||
| Задача 1 | ||||||
| x | -4 | -2 | ||||
| y | ||||||
| Задача 2 | ||||||
| x | 0,35 | 0,41 | 0,47 | 0,51 | 0,56 | 0,64 |
| y | 2,73951 | 2,3008 | 1,96864 | 1,78776 | 1,59502 | 1,3431 |
| arg=0,453 | ||||||
| Вариант 10 | ||||||
| Задача 1 | ||||||
| x | -1 | 1,5 | ||||
| y | -7 | |||||
| Задача 2 | ||||||
| x | 0,41 | 0,46 | 0,52 | 0,6 | 0,65 | 0,72 |
| y | 2,57418 | 2,32513 | 2,09336 | 1,86203 | 1,74926 | 1,62098 |
| arg=0,478 |
| Вариант 11 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -1 | -6 | ||||
| Задача 2 | ||||||
| x | 0,68 | 0,73 | 0,8 | 0,88 | 0,93 | 0,99 |
| y | 0,80866 | 0,89492 | 1,02964 | 1,20966 | 1,34087 | 1,52368 |
| arg=0,812 | ||||||
| Вариант 12 | ||||||
| Задача 1 | ||||||
| x | -9 | -7 | -4 | |||
| y | -3 | |||||
| Задача 2 | ||||||
| x | 0,11 | 0,15 | 0,21 | 0,29 | 0,35 | 0,4 |
| y | 9,05421 | 6,61659 | 4,6917 | 3,35106 | 2,73951 | 2,36522 |
| arg=0,235 | ||||||
| Вариант 13 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -1 | |||||
| Задача 2 | ||||||
| x | 0,43 | 0,48 | 0,55 | 0,62 | 0,7 | 0,75 |
| y | 1,63597 | 1,73234 | 1,87686 | 2,03345 | 2,22846 | 2,35973 |
| arg=0,645 | ||||||
| Вариант 14 | ||||||
| Задача 1 | ||||||
| x | -8 | -5 | ||||
| y | -2 | |||||
| Задача 2 | ||||||
| x | 0,02 | 0,08 | 0,12 | 0,17 | 0,23 | 0,3 |
| y | 1,02316 | 1,0959 | 1,14725 | 1,21483 | 1,3012 | 1,40976 |
| arg=0,125 | ||||||
| Вариант 15 | ||||||
| Задача 1 | ||||||
| x | -7 | -5 | -4 | |||
| y | -4 | |||||
| Задача 2 | ||||||
| x | 0,35 | 0,41 | 0,47 | 0,51 | 0,56 | 0,64 |
| y | 2,73951 | 2,3008 | 1,96864 | 1,78776 | 1,59502 | 1,3431 |
| arg=0,482 |
| Вариант 16 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -2 | |||||
| Задача 2 | ||||||
| x | 0,41 | 0,46 | 0,52 | 0,6 | 0,65 | 0,72 |
| y | 2,57418 | 2,32513 | 2,09336 | 1,86203 | 1,74926 | 1,62098 |
| arg=0,665 | ||||||
| Вариант 17 | ||||||
| Задача 1 | ||||||
| x | ||||||
| y | -2 | |||||
| Задача 2 | ||||||
| x | 0,68 | 0,73 | 0,8 | 0,88 | 0,93 | 0,99 |
| y | 0,80866 | 0,89492 | 1,02964 | 1,20966 | 1,34087 | 1,52368 |
| arg=0,774 | ||||||
| Вариант 18 | ||||||
| Задача 1 | ||||||
| x | -4 | |||||
| y | -2 | |||||
| Задача 2 | ||||||
| x | 0,11 | 0,15 | 0,21 | 0,29 | 0,35 | 0,4 |
| y | 9,05421 | 6,61659 | 4,6917 | 3,35106 | 2,73951 | 2,36522 |
| arg=0,332 | ||||||
| Вариант 19 | ||||||
| Задача 1 | ||||||
| x | -3 | -1 | ||||
| y | -1 | |||||
| Задача 2 | ||||||
| x | 0,43 | 0,48 | 0,55 | 0,62 | 0,7 | 0,75 |
| y | 1,63597 | 1,73234 | 1,87686 | 2,03345 | 2,22846 | 2,35973 |
| arg=0,736 |
Приложение 3. Численное дифференцирование. Варианты лабораторных работ
№1: f(x,y)=xy - x, a=4, b=5, c=0.7, h=0.1
Точное решение: y = 1 - 0.000100639× 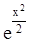
№2: f(x,y)=4x2 + 1 - 3y, a=2.6, b=4.6, c=1.8, h=0.2
Точное решение: y = 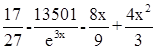
№3: f(x,y)= 1.5·x - y - 1.3, a= - 1, b=1, c=0.2, h=0.2
Точное решение: y = 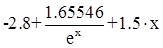
№4: f(x,y)=x + y, a=2, b=3, c=1.2, h=0.1
Точное решение: y= 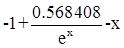
№5: f(x,y)=e-x-1 + 2y, a=0, b=0.5, c=0.3, h=0.05
Точное решение: y = 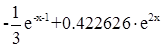
№6: f(x,y)=1.5·y + x + 1.4, a=1, b=2, c=0.9, h=0.1
Точное решение: y = 0.656994·e1.5x - 0.666667·(2.06667 + x)
№7: f(x,y)=4.1·x – y + 1.6, a=0.6, b=2.6, c=3.4, h=0.2
Точное решение: y = - 2.5 + 6.26809·e-x + 4.1·x
№8: f(x,y)= 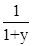 , a=1.5, b=2, c=2.1, h=0.05
, a=1.5, b=2, c=2.1, h=0.05
Точное решение: y = 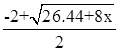
№9: f(x,y)= 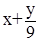 , a=2.1, b=3.1, c=2.5, h=0.1
, a=2.1, b=3.1, c=2.5, h=0.1
Точное решение: y = 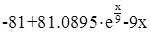
№10: f(x,y)= 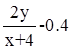 , a=3, b=5, c=1.7, h=0.2
, a=3, b=5, c=1.7, h=0.2
Точное решение: y=1.6+0.4·x-0.022449(4+x)2
№11: f(x,y)=2.5·x + y + 0.6, a=1, b=3,c=1.5,h=0.2
Точное решение:y=-3.1+2.61194·ex-2.5x
№12: f(x,y)=x + 2.5·y + 2, a=1, b=2, c=0.9, h=0.1
Точное решение: y = 0.185512·e2.5x - 0.96-0.4·x
№13: f(x,y)=2 – x - y, a=2, b=3, c=2.3, h=0.1
Точное решение: y = 3+9.60577·e-x-x
№14: f(x,y)=y + 1, a=0.1, b=0.5, c=1.25, h=0.05
Точное решение: y = - 1 + 2.03588·ex
№15: f(x,y)= 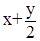 , a=-2, b=-1, c=3, h=0.1
, a=-2, b=-1, c=3, h=0.1
Точное решение: y= 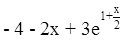
№16: f(x,y)=x2 + 0.5·y + 1, a=0, b=2, c=2.9, h=0.2
Точное решение: y=20.9·e0.5x - 18 - 8x - 2x2
№17: f(x,y)=x + y + 1.5, a=1.5, b=2.5, c=0.5, h=0.1
Точное решение: y = - 2.5 + 1.00409·ex-x
Приложение 4. Задачи оптимизации. Варианты самостоятельных работ
Задача 1. Завод выпускает обычные станки и станки с программным управлением, затрачивая на один обычный станок 200 кг стали и 200 кг цветного металла, а на один станок с программным управлением 700 кг стали и 100 кг цветного металла. Завод может израсходовать в месяц до 46 тонн стали и до 22 тонн цветного металла. Сколько станков каждого типа должен выпустить за месяц завод, чтобы объем реализации был максимальным, если один обычный станок стоит 2000 д.е., а станок с программным управлением 5000 д.е.
Задача 2. Для производства двух видов изделий А и В используется три типа технологического оборудования. На изготовление одного изделия А оборудование первого типа используется в течение 5 ч., второго - в течение 3 ч. и третьего - 2 ч. На производство одного изделия В, соответственно: 2 ч., 3 ч. и 3 ч. В плановом периоде оборудование первого типа может быть использовано в течение 505 ч., второго - 394 ч. и третьего - 348 ч. Прибыль от реализации одного изделия А равна 7 д.е., В - 4 д.е. Составить план производства, максимизирующий прибыль предприятия.
Задача 3. Для изготовления изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется сырья первого вида 15 кг, второго - 11 кг, третьего - 9 кг, а на производство одного изделия В, соответственно, 4 кг, 5 кг, 10 кг. Сырья первого вида имеется 1095 кг, второго - 865 кг, третьего - 1080 кг. Составить план производства, максимизирующий прибыль, если прибыль от реализации единицы изделия А составляет 3 д.е., В - 2 д.е.
Задача 4. Для производства изделий А и В используются три вида оборудования. При изготовлении одного изделия А оборудование первого вида занято 7 ч., второго - 6 ч. и третьего - 1 ч. При изготовлении одного изделия В, соответственно, 3 ч., 3 ч. и 2 ч. В месяц оборудование первого вида может быть занято 1365 ч., второго - 1245 ч. и третьего - 650 ч. Составить план производства, максимизирующий прибыль, если прибыль от реализации одного изделия А равна 6 д.е., изделия В - 5 д.е.
Задача 5. Для изготовления изделий А и В используется три вида сырья. На изготовление одного изделия А требуется 9 кг сырья первого вида, 6 кг сырья второго вида и 3 кг сырья третьего вида. На изготовление одного изделия В требуется, соответственно, 4 кг, 7 кг и 8 кг сырья. Производство обеспечено сырьем первого вида в количестве 801 кг, второго - 807 кг, третьего - 703 кг. Прибыль от продажи изделия А равна 3 д.е., изделия В - 2 д.е. Составить план производства, максимизирующий прибыль.
Задача 6. Завод выпускает два вида редукторов. На изготовление одного редуктора первого вида расходуется 4 тонны чугуна и 1 тонна стали, а на изготовление одного редуктора второго вида 2 тонны чугуна и 1 тонна стали. Завод располагает на месяц 160 тоннами чугуна и 120 тоннами стали. Составить месячный план производства редукторов, максимизирующий прибыль завода, если прибыль от продажи одного редуктора первого вида равна 400 д.е., а второго - 200 д.е.
Задача 7. Для производства изделий А и В используются три вида станков. На производство одного изделия А требуется 6 ч. работы станка первого вида, 4 ч. работы станка второго вида и 3 ч. работы станка третьего вида. На производство одного изделия В требуется 2 ч. работы станка первого вида, 3 ч. работы станка второго вида и 4 ч. работы станка третьего вида. Месячный ресурс работы всех станков первого вида, имеющихся на заводе равен 600 ч., всех станков второго вида - 520 ч. и всех станков третьего вида - 600 ч. Прибыль от реализации одного изделия А равна 6 д.е., изделия В - 3 д.е. Составить план производства на месяц, максимизирующий прибыль предприятия.
Задача 8. На ферме разводят нутрий и кроликов. В недельный рацион нутрий входят 17 кг белков, 11 кг углеводов и 5 кг жиров, а для кроликов эти нормы, соответственно, равны 13 кг, 15 кг и 7 кг. Доход от реализации одного кролика 20 д.е., а от реализации одной нутрии 25 д.е. Найти план разведения животных, максимизирующий доход фермы, если ферма не может расходовать в неделю более 184 кг белков, 152 кг углеводов и 70 кг жиров.
Задача 9. Для изготовления изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется 12 кг сырья первого вида, 10 - второго и 3 - третьего, а на производство одного изделия В, соответственно, 3 кг, 5 кг, 6 кг. Производство обеспечено сырьем первого вида в количестве 684 кг, второго - 690 кг и третьего 558 кг. Одно изделие А дает предприятию 6 д.е. прибыли, изделие В - 2 д.е. Составить план производства, максимизирующий прибыль предприятия.
Задача 10. Мастерская по покраске кузовов автомобилей рассчитана на покраску не более 160 кузовов в месяц. На покраску кузова “Москвича” краски расходуется 4 кг, а кузова “Волги” - 7 кг. Мастерская располагает 820 кг краски на месяц. Составить месячный план покраски автомобилей, максимизирующий прибыль мастерской, если покраска одного “Москвича” дает 30 д.е. прибыли, а одной “Волги” - 40 д.е. прибыли.
Приложение 5. Транспортная задача. Варианты самостоятельных работ
| Вариант 1 | |||||
| Вариант 2 | |||||
| Вариант 3 | |||||
| Вариант 4 | |||||
| Вариант 5 | |||||
| Вариант 6 | |||||
| Вариант 7 | |||||
| Вариант 8 | |||||
| Вариант 9 | |||||
| Вариант 10 | |||||
ЛИТЕРАТУРА.
1. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике: Учеб. Пособие для техникумов. — 2-е изд., перераб. И доп. — М.: Высш. Школа, 1990
2. Касаткин В.Н., Верлань А.Ф. Основы информатики и вычислительной техники: Проб. Учеб. Пособие для 10-11 кл. сред. Шк. — К.: Рад. Шк., 1989
3. Пулькин С.П. Вычислительная математика. Пособие для учащихся 9-10 кл. по факультативному курсу. — М.: Просвещение, 1974
4. Шамаева И.Д., Белова Т.Н. Приближенное вычисление интегралов. - // Информатика и образование, №2 1999
5. Курицкий Б. Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV – Санкт-Петербург, 1997
6. Заварыкин В. М., Житомирский В. Г., Лапчик М. П. Численные методы: Учебное пособие для студентов физ. - мат. спец. пединститутов. М.: Просвещение, 1990
7. Гасс С. Путешествие в страну линейного программирования, М. 1978
8. Волченко И. О. Вычислительная техника и программирование на алгоритмическом языке БЕЙСИК. Мурманск, 1989
Дата добавления: 2015-10-31; просмотров: 251 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Составление математической модели | | | Pierre cassée. |