Доказательство.

Лемма 2. Любая теорема теории L является тавтологией.

Доказательство. Пусть для формулы А теории L существует вывод Докажем по индукции, что ? Тавтология, i = от 1 до n По определению вывода, является аксиомой и по лемме 1 она является тавтологией.

Пусть формулы тавтология,

Рассмотрим : она является аксиомой, или получена по правилу вывода modus ponens из предыдущих формул. Если аксиома, то она является тавтологией по лемме 1. Пусть ponens из формул из формул и , i,j 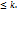По индукционному предположению, тавтологии. Пусть, на некотором наборе значений пропозициональных букв формула принимает значение 0. Тогда на этом наборе Противоречие. Следовательно тавтология. Следовательно А тавтология.

Пусть А формула, в которую входят пропозициональные буквы 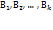. Когда нам будет необходимо подчеркнуть, от каких значений рассматривается А, будем писать , имея ввиду, что вместо пропозициональной буквы подставляется значение , i = от 1 до к. Как и раньше, будем использовать знак степени для обозначения наличия или отсутствия отрицания:

Лемма 3. Пусть - все пропозициональные буквы, которые входят в формулу А, и пусть - логические константы. Тогда

Доказательство. Докажем по индукции по числу i логических связок в формуле А. 1)

2)Пусть утверждение верно для любого i < n. Докажем для случая n логических связок в А. Формула А, в зависимости от своей логической связки, может быть одного из двух видов:

или .

А) Пусть , рассмотрим два варианты пусть . По индукционному предположению

Следовательно

Собственно теорема. Формула А формальной теории L есть тавтология тогда и только тогда, когда А – теорема теории L.

Доказательство.

Достаточность следует из леммы 2 Покажем необходимость. Пусть А тавтология. Пусть все пропозициональные буквы, которые входят в формулу А, и пусть логические константы.

По лемме 3

Поскольку А тавтология, для любых наборов , тогда: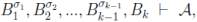

Вопрос 13. Исчисление предикатов. Основные понятия. Примеры.

Начнем с примера.

2)появились кванторы .

3) в исчислении высказываний формула была логическим законом, если принимала значение «истина» на любом наборе логических констант, подставляемых вместо пропозициональных букв. Теперь мы используем предикаты с переменными из некоторого множества, так что проверить, что формула истинна на всех наборах не так просто. Кроме того, одной и той же формуле ложно приписать различные области определения и по-разному определять истинное или ложное значение входящих в нее предикатов на данных аргументах. Здесь нам будет необходимо новое понятие интерпретация.

Будем говорить, что М вместе с сопоставленным предикатом A, B, C, D подмножествами и соответствующим «Гегелю» Элементом m есть интерпретация нашей формулы. Если задана интерпретация, то формула в этой интерпретации получает значение «Истина» или «ложь». В общем случае безотносительно интерпретации говорить значении формулы исчисления предикатов бессмысленно.

Замечание. Заметим, что наше исходное словесное рассуждение на счет сыновей Гегеля не является интерпретацией, поскольку не определена область интерпретации М.

Определение. Будем говорить, что формула тождественно истинна (логически общезначима), если ее значение «истина» в любой интерпретации.

В общем случае определение, является ли формула логически общезначимой, алгоритмически неразрешимая задача. Тем не менее в некоторых частных случаях можно доказать, что формула является тождественно истинной. Покажем это для формулы (31).

Формальная теория исчисления предикатов.

Дата добавления: 2015-10-30