Вопрос 6: Лемма о несамодвойственной функции.

Пусть

Тогда, подставляя в f вместо аргументов x и x(с крышечкой) можно получить константу.

Доказательство:

Пусть Такой набор, что

Такой набор обязан существовать, в силу несамодвойствеyности функции f.

Рассмотрим функцию тогда

Следовательно – константа.чтд.

Вопрос 7: Линейность. Замкнутость класса линейных функций. Лемма о нелинейной функции.

Пусть . Функция f – линейная, если ее полином Жегалкина имеет вид:

Обозначим как L класс всех линейных функций.

Пример: x – линейная функция не является линейной.

Утверждение: Класс функций L замкнут.

Доказательство: Рассмотрим суперпозицию ранга 1 от функций L:

А)Пусть и

Если

То =>

b) Пусть

и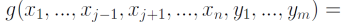

Пусть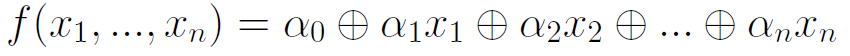

И

Тогда

Если некоторая переменная совпадает с переменной сложим коэфиценты по модулю 2. Полученный полином Жегалкина линеен. Следовательно,

Таким образом, [L] = L.

Лемма о нелинейной функции:

Пусть .

Тогда, подставляя в f вместо аргументов константы, X, Y, , и возможно, навешивая отрицание над f можно получить .

Доказательство:

Пусть

Тогда существует

Не умаляя общности, положим

Причем

Действительно, такие ,

Существуют, поскольку, если бы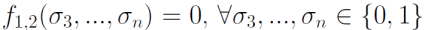

То функция f приняла бы вид

Что противоречит нашему предположению, что Рассмотрим:

Теперь определим

Тогда

Таким образом, мы получили функцию , причем

Где добавление к X и Y констант 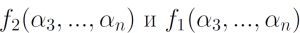равносильно навешиванию отрицания над переменной, если соответствующая константа равна 1, а добавление константы

К f означает возможное навешивание отрицания над этой функцией.

Вопрос 8:Монотонность. Замкнутость класса монотонных функций. Лемма о немонотонной функции.

Пусть

Тогда

Замечание: Существуют наборы, для которых неприменимо отношение упорядоченно-

сти, определённое выше. Так, например, наборы (0, 0, 1) и (0, 1, 0) несравнимы.

Определение 2. Функция алгебры логики

f (x 1, …, xn) называется монотонной, если для

любых двух сравнимых наборов 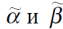выполняется инпликация.

Класс M всех монотонных функций.

Классу M принадлежат функции:

0, 1, x, xy, x ∨ y, m (x, y, z) = xy ∨ yz ∨ zx.

Классу M не принадлежат функции:

Дата добавления: 2015-10-30