
Читайте также:
|
Из этого замечания следует естественный тест для сопоставления реальных и кейнсианских теорий: просто построить регрессию выпуска на денежную массу. Подобный подход имеет длительную предысторию. Одна из первых попыток построения регрессии выпуска на денежную массу была предпринята Леонолом Андерсеном и Джерри Йорданом из Федерального Резервного Банка Сент Луиса (Andersen and Jordan, 1968). С тех пор регрессию объема выпуска на денежную массу называют Сент-Луисским уравнением.
Здесь мы рассмотрим один из примеров Сент-Луисского уравнения. Переменная в левой части – это приращение логарифма реального ВВП. Основная переменная в правой части – это приращение логарифма денежной массы, определяемой как агрегат 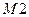 . Чтобы учесть возможность воздействия денежной массы на выпуск с лагом, в регрессию включены текущий объем денежной массы и четыре лаговых величины. Кроме этого в регрессии присутствует константа и временной тренд, позволяющий учесть тренды в росте выпуска и денежной массы. Рассматриваются поквартальные данные за период с 1959 по 1999 год.
. Чтобы учесть возможность воздействия денежной массы на выпуск с лагом, в регрессию включены текущий объем денежной массы и четыре лаговых величины. Кроме этого в регрессии присутствует константа и временной тренд, позволяющий учесть тренды в росте выпуска и денежной массы. Рассматриваются поквартальные данные за период с 1959 по 1999 год.
Был получен следующий результат:
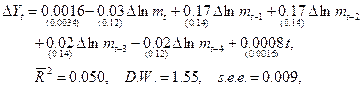 (5.40)
(5.40)
где в скобках приведены стандартные ошибки. Сумма коэффициентов перед текущим и четырьмя лаговыми значениями темпа роста денежной массы равна 0.33 при стандартной ошибке 0.11 (? Сумма равна 0,33, и стандартная ошибка, видимо, больше- надо уточнить! –В.П.). Полученная оценка означает, что однопроцентное увеличение денежной массы связано с ростом выпуска на 1/3 процента на протяжении последующего года. Нулевая гипотеза об отсутствии связи отвергается при высоком уровне значимости.
Можно ли тогда считать, что данная регрессия дает убедительное доказательство в пользу монетарных, а не реальных теорий колебаний? Нет, нельзя. Существует несколько основных проблем, связанных с построением подобных регрессий. Во-первых, причинно-следственная связь может идти не от денежной массы к выпуску, а наоборот, от выпуска к денежной массе. Простое соображение, формализованное в работе King and Plosser (1984), состоит в следующем. В ситуации, когда фирмы планируют увеличить объем производства, они могут увеличить запас денег, который будет необходим для закупки промежуточной продукции. Аналогично, домохозяйства могут увеличить запас денег, если они планируют увеличить объем покупок. Денежные агрегаты, такие как 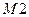 , не устанавливаются напрямую Федеральной Резервной Системой, а определяются предложением денежной базы, поведением банковской системы и частных лиц. Таким образом, изменения в спросе на деньги, обусловленные пересмотром производственных планов фирм и домохозяйств, могут привести к изменению объема денежной массы. В результате мы можем наблюдать изменения в объеме денежной массы, которые опережают изменения в выпуске, даже если сами по себе эти изменения и не приводят к изменениям выпуска.
, не устанавливаются напрямую Федеральной Резервной Системой, а определяются предложением денежной базы, поведением банковской системы и частных лиц. Таким образом, изменения в спросе на деньги, обусловленные пересмотром производственных планов фирм и домохозяйств, могут привести к изменению объема денежной массы. В результате мы можем наблюдать изменения в объеме денежной массы, которые опережают изменения в выпуске, даже если сами по себе эти изменения и не приводят к изменениям выпуска.
Вторая важная проблема состоит в том, что Сент-Луисское уравнение включает детерминанты монетарной политики. Предположим, например, что Федеральная Резервная Система подстраивает объем денежной массы, пытаясь нейтрализовать воздействие на совокупный выпуск других факторов. Тогда, если монетарные изменения обладают реальными эффектами и усилия Федеральной Резервной Системы увенчиваются успехом, мы будем наблюдать изменения в денежной массе в отсутствии изменений в выпуске (Kareken and Solow, 1963). Таким образом, так же как из наблюдаемой положительной корреляции между денежной массой и выпуском мы не можем сделать однозначный вывод, что именно изменения в денежной массе являются причиной изменений в выпуске, отсутствие данной корреляции не позволяет заключить, что денежная масса не влияет на выпуск.[22]
Третье затруднение с Сент-Луисским уравнением состоит в том, что за последние два десятилетия произошли значительные сдвиги в спросе на деньги. Некоторые из них, вероятно, связаны с инновациями на финансовых рынках и дерегулированием банковской системы, хотя их причины до сих пор еще не нашли полного объяснения.[23] Если Федеральная Резервная Система не подстраивает в полной мере предложение денег к данным шокам, модель IS-LM-AS предсказывает, что они будут порождать отрицательную связь между денежной массой и выпуском. Например, положительный шок спроса на деньги приведет к увеличению объема денежной массы, но увеличит при этом ставку процента и снизит объем выпуска. И даже если Федеральная Резервная Система реагирует на эти сдвиги, их крупномасштабный характер может привести к тому, что несколько наблюдений окажут диспропорционально большое влияние на результат.
Происходящие сдвиги спроса на деньги делают оценку зависимости выпуска от денежной массы весьма чувствительной к таким аспектам, как выбор периода времени и характеристики денежной массы. Если, например, регрессия типа (5.40) строится с использованием агрегата  вместо
вместо 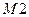 , или если берется иной период выборки, результаты меняются значительно.
, или если берется иной период выборки, результаты меняются значительно.
Вследствие этих трудностей, регрессия вида (5.40) не может быть использована для получения веских доводов в пользу монетарной либо реальной теории флуктуаций.
Дата добавления: 2015-10-30; просмотров: 144 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модифицированная кривая Филлипса, учитывающая ожидания | | | Другие доводы |