Усложнение модели

Запас земли фиксирован, а объем других природных ресурсов, в конце концов, должен сократиться. Несмотря на то, что технический прогресс позволял компенсировать ограниченность земли и природных ресурсов на протяжении последних столетий, может оказаться, что эти ограничения, в конце концов, выступят как жесткое ограничение, не допускающее дальнейший рост производства.

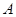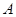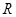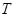В рассматриваемой модели этого не происходит ввиду того, что в анализе была использована производственная функция Кобба-Дугласа. При такой производственной функции заданное процентное изменение всегда приведет к одинаковому процентному изменению выпуска, независимо от того, насколько велико по отношению к и . Поэтому технический прогресс всегда способен компенсировать сокращение 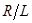и .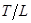

Однако это не является общим свойством производственной функции. В функции Кобба-Дугласа, эластичность замещения между факторами производства равна 1. Если эластичность замещения меньше единицы, то доля в доходе факторов, со временем становящихся более редкими, возрастает. Это легко пояснить на интуитивном уровне: если производственная функция становится более похожей на функцию Леонтьева, то роль относительно редких ресурсов возрастает. Аналогично, если эластичность замещения больше единицы, доля в доходе ресурсов, становящихся более редкими, со временем снижается. Это тоже понятно интуитивно: производственная функция становится ближе к линейной, от чего выигрывают факторы, имеющиеся в изобилии.

Сопоставим эти рассуждения с предыдущим анализом. Если мы не ограничиваемся анализом производственной функции Кобба-Дугласа, то доли доходов в выражении (1.51), показывающем замедление темпов роста, уже не постоянны, а зависят от пропорции, в которых факторы используются в производстве. При этом, если эластичность замещения меньше единицы, доли дохода природных ресурсов и земли в совокупном доходе со временем будут возрастать; будет возрастать и величина замедления. Действительно, в данном случае доля дохода наиболее медленно растущего фактора (ресурсов) стремится к единице. Замедление роста сходится к 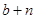. Таким образом, доход на одного работника асимптотически снижается с темпом 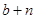, то есть с темпом снижения ресурсов на одного работника. Этот случай отражает наши апокалиптические ожидания: в долгосрочной перспективе фиксированное предложение ресурсов приводит к медленному, но неизбежному сокращению доходов.

Однако в действительности, рассмотрение более общего случая, нежели производственная функция Кобба-Дугласа, должно привести к пересмотру роли природных ресурсов не в сторону повышения, а в сторону снижения. Причина этого состоит в том, что доли доходов ресурсов и земли в совокупном доходе со временем сокращаются, а не возрастают. Мы можем записать долю дохода земли как произведение реальной арендной платы за землю на отношение количества земли к выпуску. Рентная арендная плата медленно растет, в то время, как отношение количества земли к ВВП устойчиво снижается. Аналогично, реальная стоимость ресурсов медленно снижается, снижается и доля ресурсов в ВВП. Таким образом, доля дохода ресурсов также снижается. В результате уменьшения долей доходов земли и природных ресурсов темпы роста замедляются, в меньшей степени.

Несмотря на то, что земля и природные ресурсы становились относительно более редкими, их доли в совокупном доходе со временем сокращались. Следовательно, эластичность замещения между этими факторами производства и другими должна быть больше единицы. На первый взгляд, это может показаться удивительным. Если мы рассмотрим узко определенные блага, например, книги, то возможность замещения различных факторов производства не кажется слишком высокой. Однако если учесть, что люди ценят не конкретные блага, а лишь конечное удовлетворение своих потребностей, например, накопленную информацию, то гипотеза о существовании широких возможностей для замещения становится более правдоподобной. Информацию можно хранить не только с помощью книг, но также и благодаря устной традиции, каменных дощечек, микрофильмов, видеопленки и дисков. Эти различные способы хранения информации используют капитал, ресурсы, землю и труд в разных пропорциях. Поэтому в результате сокращения количества земли и ресурсов на одного работника, экономика может переключиться на способы хранения информации, которые используют землю и природные ресурсы менее интенсивно.

Загрязнение

Сокращение количества земли и природных ресурсов на одного работника – не единственная причина, в силу которой проблемы окружающей среды могут ограничить рост. Производство приводит к загрязнению. Загрязнение сокращает выпуск, измеренный соответствующим образом. А именно, если бы наши данные о реальном выпуске учитывали все производимые продукты в ценах, отражающих их влияние на полезность, загрязнение вошло бы в эту сумму с отрицательной ценой. Кроме того, загрязнение может возрасти настолько, что начнет сокращаться выпуск, рассчитанный обычным образом. Так например, глобальное потепление может привести к сокращению выпуска ввиду изменения уровня океана и погодных условий.

Экономическая теория не дает нам оснований для оптимизма в отношении загрязнений. Коль скоро те, кто загрязняют окружающую среду, не несут издержек, связанных с загрязнением, нерегулируемый рынок приводит к чрезмерному ее загрязнению. Более того, на нерегулируемом рынке отсутствуют механизмы, которые позволили бы предотвратить экологическую катастрофу. Предположим, например, что существует некоторый критический уровень загрязнения окружающей среды, после которого наступает внезапное резкое изменение климата. Ввиду того, что эффекты загрязнения являются внешними, отсутствуют рыночные механизмы, которые не позволили бы загрязнению достичь этого уровня. Не существует даже рыночной цены чистой окружающей среды, цены, которая предупредила бы нас о том, что хорошо информированные участники рынка верят в неизбежность катастрофы.

В принципе, государственная политика, корректирующая загрязнение окружающей среды, проста. Мы должны оценить в деньгах ущерб от внешнего эффекта, и ввести налог на загрязнение, в точности равный этому ущербу. Это уравняет частные и общественные издержки, что приведет к социально оправданному уровню загрязнения.[25]

Несмотря на то, что описание оптимальной политики относительно просто, возникают серьёзные затруднения, связанные с оценкой ущерба от загрязнения. С точки зрения теории экономического роста, мы хотели бы знать, насколько сильно загрязнение замедлит темпы экономического роста, если не будет принято никаких мер со стороны государства. С точки зрения политики, мы хотели бы знать, какой уровень налога на загрязнение окружающей среды будет еще приемлемым. В случае, если налог на загрязнение политически недопустим, хотелось бы понять, превосходят ли выгоды более непосредственного регулирования его издержки. Наконец, с точки зрения нашего собственного поведения, мы хотели бы понять, насколько интенсивные усилия для сокращения загрязнения окружающей среды следует предпринимать индивидууму, заботящемуся о благосостоянии других.

Ввиду отсутствия рыночных цен, на которые можно было бы ориентироваться, экономистам, занимающимся вопросами окружающей среды, приходится начинать анализ с рассмотрения научных данных. Например, оценка глобального потепления в отсутствии государственного вмешательства с 1990 по 2050 год составляет 3 градуса по Цельсию (Nordhaus, 1992). Экономисты могут оценить, какое это окажет влияние на благосостояние. Так, эксперты по сельскому хозяйству оценили последствия глобального потепления на урожайность посевных в США. Эти исследования показали, что глобальное потепление будет иметь значительный отрицательный эффект. Однако Мендельсон, Нордхауз и Шоу (Mendelsone, Nordhaus and Shaw, 1994) отметили, что фермеры могут отреагировать на это изменением посевных культур, либо использовать землю для каких-либо других нужд. Они показали, что если учесть эти возможности для замещения, общий эффект потепления в США окажется небольшим, и, возможно, даже положительным.

После анализа различных каналов, через которые глобальное потепление может отразиться на благосостоянии, Нордхауз (Nordhaus, 1991) приходит к выводу, что чистый эффект к 2050 году для США окажется небольшим и отрицательным, эквивалентным сокращению ВВП на 1-2%. Это соответствует сокращению средних темпов роста в 1990 – 2050 гг. на 0.03 процентных пункта. После этого неудивительным кажется вывод Нордхауза о том, что радикальные меры, направленные на борьбу с глобальным потеплением (например, сокращение наполовину выбросов, создающих парниковый эффект), будет более разрушительным, чем простое невмешательство.

Используя аналогичный подход, Нордхауз (Nordhaus, 1992) пришел к выводу, что ущерб для благосостояния от других источников загрязнения выше, однако не слишком высок. Соответствующим образом измеренный темп роста, по его оценкам, снижается за счет загрязнения примерно на 0,04 процентных пункта.

Конечно, нельзя исключить, что использованные научные данные или упомянутые попытки оценить влияние загрязнения окружающей среды на благосостояние далеки от фактического положения дел. Также не исключено, что анализ более длительных промежутков времени, чем традиционные для такого рода исследований 50 или 100 лет, значительно изменят наши выводы. Однако остается фактом, что большинство экономистов, изучавших серьёзно этот вопрос, и даже те, кто изначально выступал за жесткие меры, направленные на защиту окружающей среды, пришли к выводу, что влияние загрязнения окружающей среды на темпы роста в худшем случае весьма умеренны.[26]

Задачи

1.1. Базовые свойства темпов роста. Учитывая, что темп роста переменной равен производной по времени её логарифма, докажите нижеследующие утверждения.

(а) Темп роста произведения двух переменных равен сумме темпов роста этих переменных, т.е. если 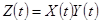, то .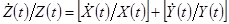

(б) Темп роста отношения двух переменных равен разности темпов роста этих переменных: если 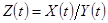, то .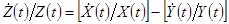

(в) Если 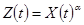, то .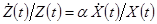

1.2. Предположим, что темп роста некоторой переменной 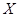постоянен и равен 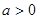на интервале от 0 до 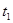, снижается до 0 в момент 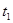, плавно возрастает с 0 до 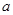на интервале от 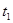до 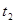, и остается на уровн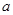е после .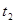

(а) Постройте график темпа роста 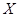как функции времени.

(б) Постройте график 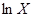как функции времени.

1.3. Опишите, как каждое из нижеследующих событий влияет на положение линий фактических и восстанавливающих инвестиций на базовой диаграмме модели Солоу.

(а) Сокращение нормы амортизации

(б) Увеличение темпов технического прогресса

(в) Рост доли дохода капитала 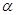в случае производственной функции Кобба-Дугласа, .

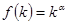(г) Рабочие прикладывают больше усилий, так что выпуск на единицу эффективного труда при заданной капиталовооруженности эффективного труда оказывается выше.

1.4. Рассмотрим экономику, в которой наблюдается технический прогресс, однако отсутствует рост населения. Изначально экономика находится на траектории сбалансированного роста. Предположим теперь, что происходит одноразовое скачкообразное увеличение численности рабочей силы.

(а) В момент увеличения численности рабочей силы, выпуск на единицу эффективного труда увеличится, уменьшится или останется неизменным? Почему?

(б) После начального изменения выпуска на единицу эффективного труда (если таковое произойдет), будет ли в дальнейшем наблюдаться увеличение или уменьшение выпуска на единицу эффективного труда? Почему?

(в) После того, как экономика вновь достигнет траектории сбалансированного роста, будет ли выпуск на единицу эффективного труда выше, ниже, или таким же, как до шока? Почему?

1.5. Предположим, что производственная функция имеет вид Кобба-Дугласа.

(а) Найдите 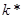, 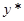и 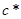как функции от параметров модел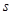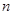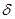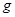и , , , и .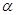

(б) Найдите 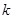, соответствующее золотому правилу.

(в) Какая норма сбережений требуется для достижения запаса капитала, соответствующего золотому правилу?

1.6. Экономика, описываемая моделью Солоу, изначально находится на траектории сбалансированного роста. Для простоты допустим, что технический прогресс отсутствует. Предположим теперь, что темп роста населения упал.

(а) Что произойдет с капиталом на одного работника, выпуском на одного работника и потреблением на одного работника на траектории сбалансированного роста?

(б) Как скажется снижение темпов роста населения на динамике выпуска (т.е. выпуска в экономике в целом, а не на одного работника)

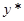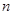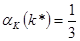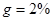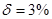1.7. Определите эластичность выпуска на единицу эффективного труда на траектории сбалансированного роста по темпу роста населения . Пусть , и , а 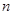сокращается с 2% до 1%. Как изменится ?

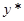1.8. Предположим, что отношение инвестиций к выпуску в Соединенных штатах непрерывно возрастает с 0,15 до 0,18. Пусть доля дохода капитала в совокупном доходе составляет .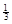

(а) Как в конце концов изменится выпуск по отношению к тому уровню, на котором он был бы без изменения отношения инвестиций к выпуску?

(б) Как в конце концов изменится потребление по отношению к тому уровню, на котором оно было бы без изменения отношения инвестиций к выпуску?

(в) Каково мгновенное воздействие изменения доли инвестиций в выпуске на потребление?

1.9. Оплата факторов в модели Солоу. Предположим, что и труд и капитал оплачиваются в соответствии с их предельными продуктами. Пусть 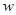обозначает 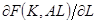, а 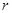обозначает .

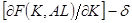(а) Покажите, что предельный продукт труда, 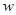, равен .

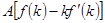(б) Покажите, что, если и труд и капитал оплачиваются в соответствии с их предельным продуктом, из условия постоянной отдачи от масштаба следует, что средства, направляемые на оплату факторов, в точности равняются выпуску, т.е. .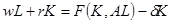

(в) Отдача от капитала 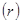, а также доли дохода труда и капитала в совокупном доходе в развитых странах примерно постоянны во времени. Выполняется ли это условие на траектории сбалансированного роста в модели Солоу? Каковы темпы роста 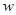и 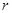на траектории сбалансированного роста?

(г) Предположим, что изначально 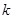меньше 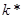. При приближении 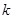к 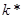, 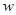растет с темпом большим, меньшим или равным темпу роста на траектории сбалансированного роста? Что происходит с ?

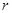1.10. Предположим, что, как и в задаче 1.9, капитал и труд оплачиваются в соответствии с их предельными продуктами. Кроме того, предположим, что доход капитала сберегается, а доход труда – потребляется. Таким образом, .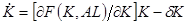

(а) Покажите, что экономика стремится к траектории сбалансированного роста.

(б) Значение 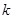на траектории сбалансированного роста больше, меньше или равно 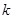, соответствующего золотому правилу?

1.11. Воплощенный технический прогресс. (На основе работ Солоу и Сато (Solow, 1956 и Sato, 1966)). Одним из свойств технического прогресса является то, что капитал, созданный к моменту 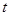, зависит от уровня технологии в момент 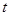и не совершенствуется за счет будущего технического прогресса. Эта гипотеза известна как гипотеза воплощенного технического прогресса (технический прогресс должен быть «воплощен» в капитале до того, как он приведет к росту выпуска). В данной задаче Вам предлагается исследовать последствия этого эффекта.

(а) Во-первых, модифицируем базовую модель Солоу, предположив, что технический прогресс воплощается в капитале, а не в труде. Для того, чтобы существовала траектория сбалансированного роста, предположим, что производственная функция имеет вид Кобба-Дугласа, 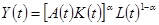. Предположим, что 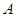растет с темпом : .

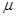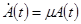Покажите, что экономика стремится к траектории сбалансированного роста, и определите темпы роста 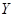и 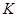на траектории сбалансированного роста. (Подсказка: покажите, что мы можем записать 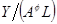как функцию от 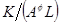, где 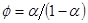, после чего проведите анализ динамики .)

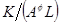(б) Теперь введем гипотезу воплощенного технического прогресса. Предположим, что производственная функция имеет вид 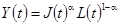, где – эффективный запас капитала. Динамика задается выражением 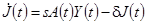. Множитель 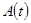в последнем выражении показывает, что инвестиции в момент 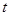зависят от технологии в момент .

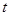Покажите, что экономика стремится к траектории сбалансированного роста. Каковы темпы роста 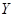и 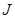на траектории сбалансированного роста? (Подсказка: обозначьте 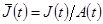, после чего воспользуйтесь тем же подходом, что и в пункте (а), анализируя динамику 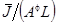вместо ).

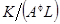(в) Какова эластичность выпуска по 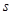на траектории сбалансированного роста?

(г) Какова скорость сходимости к траектории сбалансированного роста в ее окрестности?

(д) Сравните результаты пунктов (в) и (г) с соответствующими результатами в модели Солоу.

1.12. Рассмотрим модель Солоу на траектории сбалансированного роста. Используем калькуляцию роста, представленную в разделе 1.7.

(а) Какая часть роста выпуска на одного работника происходит за счет роста капитала на одного работника? Какая часть роста выпуска происходит за счет технического прогресса?

(б) Как бы Вы могли сопоставить свой ответ на пункт (а) с тем, что модель Солоу объясняет существование положительного темпа роста выпуска на одного работника только техническим прогрессом?

1.13. (а) В модели конвергенции и ошибок измерения, в уравнениях (1.38) и (1.39), предположим, чт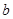о равно 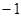. Даст ли регрессия 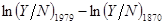на 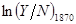смещенную оценку 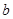? Объясните.

(б) Предположим, что существует ошибка измерения в выпуске на душу населения в 1979, а не в 1870 году. Даст ли регрессия 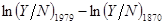на 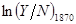смещенную оценку 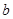? Объясните.

1.14. Покажите, как получается выражение (1.50). (Подсказка: используйте подход, аналогичный тому, что использовался для вывода выражений [1.47] и [1.48].)

[1] Мэддисон (Maddison, 1995) приводит и обсуждает данные о динамике реального дохода на протяжении новой истории. Значительная доля неопределенности при оценке масштабов долгосрочного роста связана с динамикой не номинального дохода, а индекса цен, необходимого для пересчета номинальных величин в реальные. Появление новых товаров или изменение качества уже имеющихся сложно перевести в количественные индексы. Традиционные индексы цен практически не позволяют провести хорошую оценку. См. обсуждение соответствующих проблем и анализ смещенности традиционных индексов цен в работах Нордхаус (Nordhaus, 1997) и в Боскин, Далбержер, Гордон, Грилихес и Джоргенсон (Boskin, Dulberger, Gordon, Griliches and Jorgenson, 1998).

[2] Межстрановые сравнения реального дохода – нетривиальная задача, однако она значительно проще, чем сравнение доходов для разных периодов времени. Базовым источником межстрановых данных о реальном доходе являются таблицы «Penn World Tables». Саммерс и Хестон (Summers and Heston1991) описывают эти данные и обсуждают некоторые проблемы, связанные с межстрановыми сравнениями. Наиболее свежая версия этих данных доступна в Национальном Бюро Экономических Исследований на веб-сайте http://www.nber.org

[3] Джонс (Jones, 1998) предлагает анализ экономического роста на более простом уровне, чем уровень данной книги. Барро и Сала-и-Мартин (Barro and Sala-i-Martin1998), а так же Агион и Ховитт (Aghion and Howitt1998) излагают теорию на несколько более продвинутом уровне.

[4] Модель Солоу (иногда называемая моделью Солоу-Свана) была разработана Робертом Солоу (Solow, 1956) и Т.В. Сваном (Swan, 1956).

[5] Если знания входят в форме 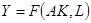, то технический прогресс является воплощенным в капитале. В случае 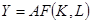технический прогресс является нейтральным по Хиксу.

[6] Через 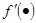обозначена первая производная функции 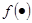, а через 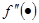- вторая производная.

* Эти условия обеспечивают существование стационарных режимов (см. ниже). (Примеч. науч. ред.).

[7] Заметим, что для производственной функции Кобба-Дугласа нет принципиальной разницы между техническим прогрессом, воплощенным в труде, воплощенным в капитале, или нейтральным по Хиксу. Например, чтобы переписать (1.5) в форме, предполагающей нейтральность технического прогресса по Хиксу, просто переобозначим 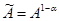; тогда .

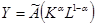[8] Альтернативой является дискретное время, когда переменные определены только на определенные даты (как правило, 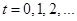). Выбор между непрерывным и дискретным временем обычно осуществляется из соображений удобства. В частности, выводы из модели Солоу принципиально не изменятся, если мы переформулируем ее в дискретном времени, однако проще проводить анализ в непрерывном времени.

* Иногда в русскоязычной литературе различают темп роста какой-либо переменной 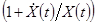и темп её прироста 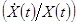. В данной книге темпом роста называется величина 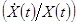. Это лучше согласуется с традицией теории экономического роста (прим. переводчика).

* Мы, таким образом, нашли решения уравнений (1.8) и (1.9) (прим. науч. ред.).

[9] В задачах 1.1 и 1.2 рассмотрены еще несколько базовых свойств темпа роста

[10] Темп роста 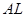равен 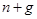, поскольку темп роста произведения двух переменных равен сумме их темпов роста. См. задачу 1.1.

[11] Если начальное значение равно нулю, то остается равным нулю навсегда. В дальнейшем анализе мы игнорируем такую возможность.

[12] Динамика экономики США и экономики многих других индустриальных стран на протяжении последнего столетия в общих чертах достаточно хорошо описывается траекторией сбалансированного роста модели Солоу. Темпы роста труда, капитала, и выпуска были примерно постоянны. Темпы роста выпуска и капитала примерно были примерно равны (т.е. отношение капитала к выпуску было примерно постоянным), и превышали темпы роста труда (поэтому выпуск на одного работника и капитал на одного работника возрастали). Зачастую принимается как данное, что экономики этих стран можно рассматривать как экономики, описываемые моделью Солоу, и находящиеся на траектории сбалансированного роста. Однако Джонс (Jones, 1999а) показывает, что детерминанты уровня дохода на траектории сбалансированного роста, на самом деле, далеко не постоянны в этих экономиках, и поэтому сходство между ними и траекториями сбалансированного роста в модели Солоу обманчиво. Мы вернемся к этому вопросу в разделе 3.3.

* Это описание не вполне точно: капиталовооруженность не достигает нового значения , а лишь неограниченно приближается к нему. (Примеч. науч. ред.).

[13] При достаточно большом увеличении нормы сбережений, 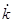растет на некотором интервале времени после 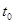, а затем начинает снижаться до нуля.

[14] Так как темп роста переменной равен производной по времени её логарифма, графики логарифмов обычно проще интерпретировать, чем графики абсолютных величин. Если, например, переменная растет с постоянным темпом, графиком динамики логарифма этой переменной будет прямая линия. Поэтому на рисунке 1.5 вместо динамики выпуска на одного работника, показана динамика его логарифма.

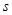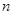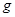[15] Эта техника известна как неявное дифференцирование. Хотя уравнение (1.22) не позволяет явным образом получить как функцию от , , , и 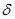, оно все же определяет зависимость от этих переменных. Поэтому мы можем продифференцировать данное уравнение по 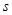, и выразить из полученного соотношения .

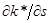[16] В предыдущем разделе мы показали, что увеличение 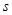приводит к росту . Проверим, что этот факт также следует из соотношения (1.24). Заметим, что 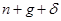- это наклон линии восстанавливающих инвестиций, а 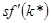- наклон линии фактических инвестиций в точке . Так как в точке наклон линии фактических инвестиций меньше наклона линии восстанавливающих инвестиций (см. Рис. 1.2), то знаменатель выражения (1.24) положителен, следовательно .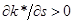

[17] Если значение какой-то переменной (в данном случае 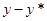) уменьшается с постоянным (отрицательным) темпом роста, то это значение сокращается вдвое за число лет, приблизительно равное частному от деления 70 на темп роста в процентах. Аналогично, удвоение переменной с положительным темпом роста происходит за (70 деленное на темп роста) лет. Следовательно, период полужизни (известный в физике как период полураспада) составляет примерно 70/(4% в год), или около 18 лет. Если быть более точными, полураспад, 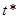, определяется из решения уравнения 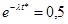, где 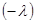– темп роста. Прологарифмировав это выражение, получаем .

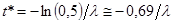[18] Эти результаты получены из разложения в ряд Тейлора в окрестности траектории сбалансированного роста. Следовательно, формально мы можем судить лишь о последствиях сравнительно небольших отклонений. В общем случае нет ответа на вопрос, дает ли разложение в ряд Тейлора хорошее приближение для более значительных отклонений. В случае модели Солоу с любой обычно используемой производственной функцией и при не слишком больших изменениях параметров (вроде тех, которые мы рассмотрели) разложение в ряд Тейлора дает достаточно точные оценки.

* В этих рассуждениях предполагается, что обе сравниваемые экономики характеризуются одной и той же производственной функцией с постоянной эластичностью. В этом случае нужное соотношение можно получить, интегрируя равенство 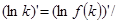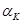, вытекающее из определения эластичности (примеч. науч. ред.).

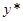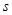[19] Можно провести аналогичные рассуждения для нормы сбережений, темпов роста населения, и других факторов, определяющих капиталовооруженность. Например, эластичность по равна 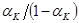(см. [1.27]). Следовательно, можно объяснить десятикратные различия в доходах на одного работника различиями в нормах сбережения 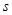, только если эти последние отличаются в в 100 раз при 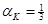и в 10 раз при 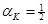. Наблюдаемые различия в нормах сбережения значительно меньше этих величин.

[20] Можно попытаться избежать этого вывода, если использовать производственную функцию, в которой предельная производительность капитала снижалась бы не так быстро, как в случае Кобба-Дугласа. Этот подход сталкивается с двумя серьезными проблемами. Во-первых, при таком подходе оказывается, что предельная производительность капитала примерно одинакова в бедных и богатых странах, а значит, доля дохода капитала должна быть значительно больше в богатых странах. Во-вторых, эта гипотеза приводит к заключению, что реальная заработная плата лишь незначительно выше в богатых странах, чем в бедных. Эти следствия сильно противоречат фактам.

[21] Баумоль рассматривал выпуск на одного работающего, а не выпуск на душу населения. Этот выбор слабо влияет на полученный результат.

[22] Включить в выборку все страны, которые были хотя бы так же богаты, как Япония, невозможно, так как большая часть мира в 1870 году была богаче, чем Япония. Кроме того, следует учитывать изменения территориальных границ. Де Лонг выбрал для анализа границы 1979 года. Поэтому его оценки доходов в 1870 году основаны на оценке средних доходов в географических регионах, определенных границами 1979 года.

* bgp – сокращение от «balanced growth path», что переводится, как «траектория сбалансированного роста» (прим. переводчика).

[23] В данных рассуждениях допущена одна неточность. Если значение выражения 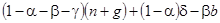отрицательно, условие 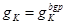выполняется только для отрицательных значений 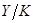. А утверждение о том, что 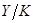сокращается, когда 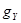меньше 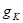, не выполняется для отрицательных значений 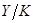.Таким образом, если значение выражения 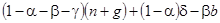отрицательно, экономика стремится не к описанной в тексте траектории сбалансированного роста, а к ситуации, в которой 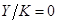, а . 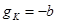Однако для любых правдоподобных значений параметров значение выражения 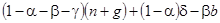положительно. Следовательно, данное усложнение не имеет особого значения.

[24] См. задачу 1.14.

[25] Альтернатива – определить социально оптимальный уровень загрязнения и провести аукцион среди участников на право загрязнения окружающей среды в данном объеме. Классический анализ выбора между контролем цен и контролем количества представлен в работе Вейцмана (Weitzman, 1974).

[26] Это не означает, что природная среда в любых случаях не имеет значения для долгосрочного роста. Брандер и Тейлор (Brander and Taylor, 1998) показали, что остров Пасхи испытал катастрофические последствия влияния природных факторов, описанных Мальтусом, в период между поселением около 400 г. и приходом европейцев в 1700-х гг. По мнению этих авторов, другие примитивные сообщества также могут испытывать подобные катастрофы.

Дата добавления: 2015-10-30