Влияние на потребление

Если бы мы ввели в модель домашние хозяйства, тогда их благосостояние зависело бы не от выпуска, а от потребления: инвестиции это лишь фактор производства в будущем. Следовательно, для анализа многих вопросов мы более заинтересованы в анализе динамики потребления, чем динамики выпуска.

Потребление на единицу эффективного труда равняется выпуску на единицу эффективного труда 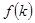, умноженному на норму потребления 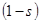. Так как 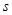меняется скачком в момент 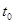, а - нет, потребление на единицу эффективного труда скачкообразно уменьшается. Затем потребление растет, так как растет , а 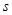остается на высоком уровне. Это показано на последнем графике рисунка 1.5.

В общем случае не ясно, превысит ли потребление свой первоначальный уровень. Обозначим через - потребление на единицу эффективного труда на траектории сбалансированного роста. Очевидно, равно выпуску на единицу эффективного труда, , за вычетом инвестиций на единицу эффективного труда, 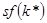. На траектории сбалансированного роста фактические инвестиции равняются восстанавливающим, . Следовательно,

(1.19)

Величина задается нормой сбережений 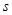, а также другими параметрами модел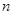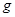и: , , и 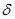; значит, мы можем записать 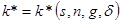. Тогда из выражения (1.19) получаем:

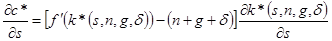(1.20)

Мы знаем, что рост 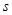приводит к увеличению . Следовательно, в зависимости от того, больше или меньше предельная отдача от капитала 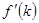, чем , увеличение нормы сбережений может приводить как к увеличению, так и к уменьшению потребления в долгосрочной перспективе. Если увеличивается, то для удержания на более высоком уровне следует увеличить инвестиции (на единицу эффективного труда) на величину , умноженную на изменение . Если меньше, чем , то приращения выпуска, достигнутого за счет роста капитала, недостаточно для того, чтобы удержать запас капитала на новом, более высоком уровне. В этом случае потребление должно снизиться, чтобы удержать более высокий запас капитала. Если превышает , то приращение выпуска больше, чем требуется для удержания на новом уровне, и потребление увеличивается.

Производная может быть больше или меньше, чем . Это показано на рисунке 1.6. На рисунке изображены не только 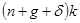и 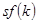, но также и 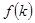. На траектории сбалансированного роста потребление равно выпуску за вычетом восстанавливающих инвестиций; таким образом, определяется расстоянием между 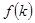и 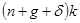. На верхнем графике меньше, чем , поэтому увеличение нормы сбережений приводит к сокращению потребления даже когда экономика достигает новой траектории сбалансированного роста. На среднем графике наблюдается обратная картина, и увеличение 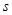приводит к росту потребления в долгосрочной перспективе.

Рисунок 1.6. Выпуск, инвестиции и потребление на траектории сбалансированного роста.

На нижнем графике в точности равняется 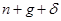: лини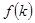и и 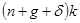параллельны друг другу в точке . В этом случае предельное изменение 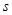не воздействует на потребление в долгосрочной перспективе, а потребление находится на уровне, максимальном среди всех возможных траекторий сбалансированного роста. Это значение называется запасом капитала, соответствующим золотому правилу. Мы обсудим золотое правило накопления капитала в главе 2. В частности, мы ответим на вопрос, является ли запас капитала, соответствующий золотому правилу, желательным для экономики, и существуют ли ситуации, когда децентрализованная экономика с эндогенной нормой сбережения стремится к этому запасу. Разумеется, в модели Солоу, где норма сбережения экзогенна, не существует причин ожидать, что запас капитала на траектории сбалансированного роста будет соответствовать золотому правилу.

Дата добавления: 2015-10-30