Динамика модели

Теперь мы хотим определить поведение только что описанной экономики. Эволюция двух из трех факторов производства, – труда и знаний, – задается экзогенно. Следовательно, чтобы определить поведение экономики, мы должны проанализировать поведение третьего фактора, капитала.

Динамика

Ввиду того, что экономика со временем растет, оказывается значительно проще сосредоточиться на анализе динамики капиталовооруженности эффективного труда , чем на динамике запаса капитала 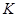. Так как 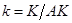, мы можем применить правило дифференцирования дроби:

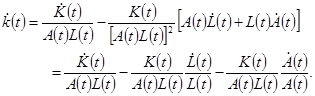(1.16)

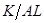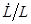Выражение - это просто . Согласно (1.8) и (1.9), и 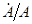равны, соответственно, 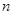и 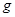. Величину 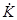находим из (1.15). Подставив эти выражения в (1.16), получим:

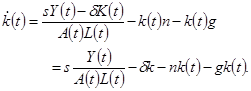(1.17)

Учитывая, что равно 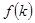, имеем:

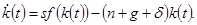(1.18)

Выражение (1.18) является основным уравнением динамики модели Солоу. Оно показывает, что изменение капиталовооруженности эффективного труда во времени определяется двумя слагаемыми. Первое слагаемое 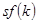– это фактические инвестиции на единицу эффективного труда. Второе слагаемое 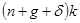– это восстанавливающие инвестиции, т.е. объем инвестиций, который должен быть произведен, чтобы удержать на существующем уровне. Имеются две причины, по которым необходим некоторый объем инвестиций для удержания на постоянном уровне. Во-первых, существующий капитал амортизируется; поэтому для поддержания на заданном уровне его объема, капитал должен обновляться. Это объясняет роль слагаемого 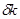в выражении (1.18). Во-вторых, количество эффективного труда растет. Поэтому инвестиции, достаточные для поддержания на заданном уровне запаса капитала 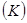недостаточны для того, чтобы поддерживать на заданном уровне капиталовооруженность эффективного труда 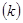. Эффективный труд растет с темпом 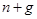, следовательно, чтобы оставить неизменным , запас капитала также должен расти с темпом 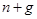.[10] Это объясняет роль слагаемого 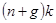в выражении (1.18).

Если фактические инвестиции на единицу эффективного труда превышают восстанавливающие инвестиции, то растет. Если фактические инвестиции на единицу эффективного труда меньше восстанавливающих инвестиций, то падает. А когда они равны между собой, переменная постоянна во времени.

Рисунок 1.2 Фактические и восстанавливающие инвестиции

На рисунке 1.2 изображена зависимость рассмотренных двух слагаемых, задающих 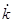, как функций от . Восстанавливающие инвестиции 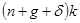пропорциональны . Фактические инвестиции 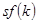– это константа, умноженная на выпуск на единицу эффективного труда.

Так как 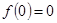, фактические инвестиции равны восстанавливающим в точке 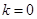. Из условий Инады следует, что при 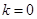производная 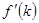велика, т.е., кривая 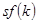имеет более крутой наклон, чем прямая 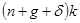. Поэтому при маленьких значениях фактические инвестиции превышают восстанавливающие. Из условия Инады также следует, что 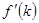стремится к нулю с увеличением . Значит, в некоторой точке наклон кривой фактических инвестиций оказывается меньше наклона прямой восстанавливающих инвестиций. Следовательно, эти линии должны где-то пересечься. Наконец, условие 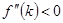гарантирует, что для 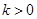эти линии пересекаются только один раз. Обозначим через - значение в той самой точке, где фактические инвестиции равны восстанавливающим.

Рисунок 1.3 Фазовая диаграмма для в модели Солоу.

Рисунок 1.3 обобщает полученную информацию посредством фазовой диаграммы, на которой отражена зависимость 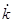от . Если в начальный момент времени меньше, чем , то фактические инвестиции больше восстанавливающих, 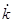положительна, и растет. Если больше , то 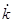отрицательна. Если равно , то 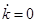. Следовательно, независимо от начального значения, стремится к .[11]

Дата добавления: 2015-10-30