
Читайте также:
|
Заключительным этапом, завершающим построение регрессионной модели, является интерпретация полученного уравнения регрессии, то есть перевод его с языка статики и математики на язык экономиста. Интерпретация начинается с выяснения, как каждый факторный признак, входящий в модель, влияет на величину результативного признака. Чем больше величина коэффициента  регрессии, тем сильнее фактор
регрессии, тем сильнее фактор  влияет на результативный признак
влияет на результативный признак  . Знаки коэффициентов регрессии
. Знаки коэффициентов регрессии  говорят о характере влияния на результативный признак. Если коэффициент
говорят о характере влияния на результативный признак. Если коэффициент  имеет знак (+), то с увеличением данного фактора
имеет знак (+), то с увеличением данного фактора  результативный фактор
результативный фактор  возрастает. Если коэффициент
возрастает. Если коэффициент  имеет знак (-), то с увеличением данного фактора
имеет знак (-), то с увеличением данного фактора  результативный признак уменьшается. Интерпретация знаков зависит от экономической сущности результативного признака. Если величина результативного признака должна изменяться в сторону увеличения (объем реализованной продукции, фондоотдача, производительность труда и т.д.), то плюсовые знаки коэффициентов
результативный признак уменьшается. Интерпретация знаков зависит от экономической сущности результативного признака. Если величина результативного признака должна изменяться в сторону увеличения (объем реализованной продукции, фондоотдача, производительность труда и т.д.), то плюсовые знаки коэффициентов  свидетельствуют о положительном влиянии соответствующих факторов. Если величина результативного признака изменяется в сторону снижения (себестоимость продукции, материалоемкость, простои оборудования и т.д.), то в этом случае положительное влияние на результативный признак будут оказывать факторы, коэффициенты, которых отрицательны.
свидетельствуют о положительном влиянии соответствующих факторов. Если величина результативного признака изменяется в сторону снижения (себестоимость продукции, материалоемкость, простои оборудования и т.д.), то в этом случае положительное влияние на результативный признак будут оказывать факторы, коэффициенты, которых отрицательны.
Если экономический анализ подсказывает, что факторный признак должен влиять положительно, а коэффициент при нем имеет знак (-), то необходимо проверить расчеты. Так получается за счет допущенных ошибок при решении и в силу наличия взаимосвязей между факторными признаками, включенными в модель, влияющих в совокупности на результативный признак.
 При построении регрессионной модели можно рекомендовать следующий алгоритм выполнения операций (рис.12):
При построении регрессионной модели можно рекомендовать следующий алгоритм выполнения операций (рис.12):
Контрольные вопросы.
1. Рассказать о механизме включения факторных признаков в модель множественной линейной регрессии.
2. Как найти коэффициенты  ,
,  ,
,  уравнения регрессии
уравнения регрессии  ?
?
3. Записать модельное уравнение множественной линейной регрессии для случая, когда в модель включено четыре фактора.
4. Записать систему нормальных уравнений для уравнения  .
.
5. Как определяется надежность коэффициентов уравнения множественной линейной регрессии?
6. Как решается вопрос об измерении тесноты связи между факторными и результативными признаками в случае множественной линейной регрессии?
7. Как осуществляется корректировка множественного коэффициента корреляции?
8. Как определить степень влияния каждого факторного признака в отдельности, включенного в модельное уравнение множественной линейной регрессии, на изменение результативного признака?
9. Рассказать, как осуществляется проверка адекватности модели множественной линейной регрессии.
10. Рассказать об экономической интерпретации уравнения множественной линейной регрессии.
Лабораторная работа №6.
Построение модели множественной
линейной регрессии.
Цель работы: овладение способами построения модели множественной линейной регрессии, выработка умений и навыков нахождения параметров уравнения, оценки надежности уравнения регрессии и его параметров, проведения экономической интерпретации полученных результатов.
Содержание работы: на основании опытных данных требуется:
Определить форму связи между факторными и результативными признаками, построив корреляционные поля на плоскости для каждой пары факторов. Записать уравнение модели множественной регрессии.
Произвести отбор факторов, включаемых в модель.
Определить тесноту связи между факторами, включенными в модель множественной линейной регрессии.
Найти оценки уравнения регрессии по методу наименьших квадратов.
Проверить адекватность полученного модельного уравнения регрессии тремя способами:
– с помощью коэффициента детерминации  ;
;
– по критерию Фишера;
– с помощью средней ошибки аппроксимации.
Определить воздействие неучтенных в модели факторов.
Дать экономическую интерпретацию найденных оценок уравнения регрессии.
Задачи. Исходные данные для признаков  ,
,  ,
, 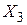 ,
,  приведены в табл. 40:
приведены в табл. 40:
| Таблица 40 | ||||||||||
| Признаки | Значение признаков на различных НГДУ | |||||||||

| 0,92 | 0,93 | 0,89 | 0,90 | 0,90 | 0,89 | 0,92 | 0,91 | 0,93 | 0,89 |

| ||||||||||
| ||||||||||
|
В таблице обозначено:  — коэффициент эксплуатации скважин;
— коэффициент эксплуатации скважин;  — дебит скважин (тн/сут.);
— дебит скважин (тн/сут.); 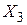 — уровень автоматизации труда (%);
— уровень автоматизации труда (%);  — производительность труда (тн/чел.).
— производительность труда (тн/чел.).
Определим форму связи. Для чего строим корреляционные поля (рис. 13-18).

Рис. 13

Рис. 14

Рис. 15

Рис. 16

Рис. 17

Рис. 18
По построенным корреляционным полям можно предположить, что зависимость между факторными признаками  ,
,  ,
, 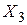 и результативным признаком
и результативным признаком  может носить прямолинейный характер. Решим вопрос о включении факторных признаков
может носить прямолинейный характер. Решим вопрос о включении факторных признаков  ,
,  ,
, 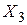 в уравнение линейной регрессии. Найдем коэффициенты парной корреляции по формуле (53). Предварительно составим расчетную таблицу 41. Пользуясь таблицей 41 и формулами (49) — (50), находим:
в уравнение линейной регрессии. Найдем коэффициенты парной корреляции по формуле (53). Предварительно составим расчетную таблицу 41. Пользуясь таблицей 41 и формулами (49) — (50), находим:
 ,
, 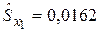 .
.
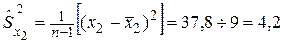 ,
,  .
.
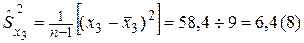 ,
,  .
.
 ,
,  .
.
 .
.
Табл.
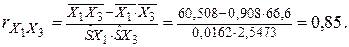

По найденным коэффициентам парной корреляции видно, что сильно коррелируют между собой факторы  или
или 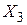 .Для решения вопроса о том, какой из факторов
.Для решения вопроса о том, какой из факторов  или
или 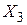 следует исключить из модели множественной линейной регрессии, вычислим коэффициенты парной корреляции
следует исключить из модели множественной линейной регрессии, вычислим коэффициенты парной корреляции  и
и  :
:


Так как  ,то между признаками
,то между признаками  и
и  связь сильнее, чем между
связь сильнее, чем между 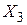 и
и  .Этот факт подтверждается путем вычисления коэффициентов частной корреляции
.Этот факт подтверждается путем вычисления коэффициентов частной корреляции 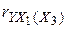 и
и  по формуле (104):
по формуле (104):


Поэтому из модели множественной линейной регрессии исключаем фактор 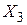 . Тогда в модель будут включены факторы
. Тогда в модель будут включены факторы  и
и  и уравнение регрессии запишется в виде
и уравнение регрессии запишется в виде
 .
.
Включение фактора  в модель обосновано значимостью коэффициента парной корреляции
в модель обосновано значимостью коэффициента парной корреляции  :
:

Для выяснения вопроса о силе линейной связи между факторами, включенными в модель, вычисляем множественный коэффициент корреляции R по формуле (100):

Так как в нашем примере объем выборки небольшой ( ), то произведем корректировку R по формуле (102):
), то произведем корректировку R по формуле (102):

Проверяем значимость  по критерию Стьюдента. Вычисляем среднеквадратическую ошибку
по критерию Стьюдента. Вычисляем среднеквадратическую ошибку  по формуле (103):
по формуле (103):

Вычисляем статику

По таблице критических точек распределения Стьюдента при уровне значимости 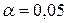 с числом степеней свободы
с числом степеней свободы  находим
находим  Так как
Так как  , то делаем вывод, что
, то делаем вывод, что  значим.
значим.
Для нахождения оценок  ,
,  ,
,  уравнения регрессии
уравнения регрессии  решаем систему нормальных уравнений по формуле (91):
решаем систему нормальных уравнений по формуле (91):
 (112)
(112)
Решив эту систему, получаем  ,
,  ,
,  .
.
Тогда уравнение регрессии, устанавливающее зависимость производительности труда  от коэффициента эксплуатации
от коэффициента эксплуатации  и дебита скважин
и дебита скважин  запишется в виде
запишется в виде  .
.
Проверяем адекватность уравнения регрессии. Используем коэффициент детерминации  , полагая
, полагая 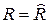 . Для полученной модели
. Для полученной модели  . Это означает, что полученная модель приблизительно на 66% объясняет изменение производительности труда в зависимости от изменения включенных в модель факторов
. Это означает, что полученная модель приблизительно на 66% объясняет изменение производительности труда в зависимости от изменения включенных в модель факторов  и
и  , что является не плохим показателем.
, что является не плохим показателем.
Проведем проверку модели на адекватность по критерию Фишера-Снедекора. Найдем статистику  по формуле (110), полагая в ней
по формуле (110), полагая в ней 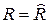 :
:
 . По таблице критических точек распределения Фишера-Снедекора при уровне значимости
. По таблице критических точек распределения Фишера-Снедекора при уровне значимости  и числах степеней свободы
и числах степеней свободы  ,
,  (p — число факторов
(p — число факторов  , включенных в модель, n — объем выборки) находим
, включенных в модель, n — объем выборки) находим  . Так как
. Так как  , то найденное уравнение регрессии, устанавливающее зависимость производительности труда на десяти нефтегазодобывающих управлениях (НГДУ) от коэффициента эксплуатации скважин
, то найденное уравнение регрессии, устанавливающее зависимость производительности труда на десяти нефтегазодобывающих управлениях (НГДУ) от коэффициента эксплуатации скважин  и дебита скважин
и дебита скважин  , значимо описывает опытные данные и может быть принято для руководства.
, значимо описывает опытные данные и может быть принято для руководства.
Оценим адекватность уравнения регрессии по средней ошибке аппроксимации  , которую вычислим по формуле (111):
, которую вычислим по формуле (111):
 .
.
Для нахождения суммы, входящей в формулу, составляем расчетную табл. 42.
| Таблица 42 | |||
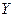
| 
| 
| 
|
| 35,2 | 0,2 | 0,000114 | |
| 36,8 | 0,8 | 0,017778 | |
| 31,5 | 0,5 | 0,005952 | |
| 33,8 | 0,8 | 0,019394 | |
| 32,7 | 1,3 | 0,049706 | |
| 32,6 | 0,6 | 0,008 | |
| 36,3 | 1,7 | 0,076053 | |
| 34,7 | 0,7 | 0,014412 | |
| 37,1 | 0,1 | 0,00027 | |
| 32,2 | 0,8 | 0,019394 | |
| 0,211073 |
По табл. 42 находим:
 . Среднеквадратическая ошибка небольшая, что дает основание считать, что построенная модель адекватно описывает опытные данные.
. Среднеквадратическая ошибка небольшая, что дает основание считать, что построенная модель адекватно описывает опытные данные.
Итак, все три метода проверки модели на адекватность подтвердили гипотезу о том, что уравнение регрессии  в целом статистически значимо и хорошо соответствует данным наблюдений.
в целом статистически значимо и хорошо соответствует данным наблюдений.
Дадим экономическую интерпретацию найденных коэффициентов уравнения регрессии. Значение свободного члена  характеризует влияние неучтенных в модели факторов, в частности фактора
характеризует влияние неучтенных в модели факторов, в частности фактора 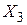 (уровень автоматизации труда). Знак минус говорит о том, что отсутствие этого фактора в модели отрицательно сказывается на повышении производительности труда. Величина коэффициента
(уровень автоматизации труда). Знак минус говорит о том, что отсутствие этого фактора в модели отрицательно сказывается на повышении производительности труда. Величина коэффициента  показывает, что при увеличении коэффициента эксплуатации на 0,01 производительность труда увеличивается в среднем на 86,3271 тн/чел. Коэффициент
показывает, что при увеличении коэффициента эксплуатации на 0,01 производительность труда увеличивается в среднем на 86,3271 тн/чел. Коэффициент  показывает, что при увеличении дебита скважин на одну тонну производительность труда увеличивается в среднем на 0,360611 тн/чел.
показывает, что при увеличении дебита скважин на одну тонну производительность труда увеличивается в среднем на 0,360611 тн/чел.
Варианты заданий к лабораторной работе № 6.
Варианты №1-№10
Данные экспериментального определения производительности труда ( ) в зависимости от коэффициента эксплуатации скважин (
) в зависимости от коэффициента эксплуатации скважин ( ), дебита скважин (
), дебита скважин (  ), уровня автоматизации труда (
), уровня автоматизации труда (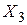 ) приведены в табл. 43. Пользуясь данными табл. 43, выполнить задание (по образцу приведенного выше примера) по вариантам, номера предприятий (НГДУ) для которых указаны в табл. 44.
) приведены в табл. 43. Пользуясь данными табл. 43, выполнить задание (по образцу приведенного выше примера) по вариантам, номера предприятий (НГДУ) для которых указаны в табл. 44.
| Таблица 43 | ||||||||||||||||
| Факторы | Значения факторов на различных НГДУ | |||||||||||||||
| Номера НГДУ | ||||||||||||||||

| 0,93 | 0,95 | 0,94 | 0,89 | 0,91 | 0,90 | 0,92 | 0,93 | 0,89 | 0,90 | 0,90 | 0,89 | 0,92 | 0,91 | 0,9 | 0,89 |

| ||||||||||||||||

| ||||||||||||||||
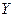
|
Здесь:  – коэффициент эксплуатации скважин (в долях),
– коэффициент эксплуатации скважин (в долях),
 – дебит скважин (тн/сут.),
– дебит скважин (тн/сут.),
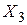 – уровень автоматизации труда (%),
– уровень автоматизации труда (%),
 – производительность труда (тн/чел.).
– производительность труда (тн/чел.).
| Таблица 44 | |||
| Варианты | Номера предприятий | Варианты | Номера предприятий |
| 1-3, 7-12, 16 | 4-6, 10-16 | ||
| 1-3, 7-9, 13-16 | 1-6, 13-16 | ||
| 1-6, 10-12, 16 | 7-16 | ||
| 1-3, 10-16 | 4-9, 13-16 | ||
| 4-12, 16 | 1-9, 16 |
Вариант №11.
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость среднего дебита действующих скважин по нефти ( ), от фонда действующих нагнетательных скважин на конец года (
), от фонда действующих нагнетательных скважин на конец года ( ), средней приемистости нагнетательных скважин (
), средней приемистости нагнетательных скважин ( ) и фонда механизированных скважин на конец года (
) и фонда механизированных скважин на конец года (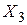 ) приведены в табл. 45.
) приведены в табл. 45.
| Таблица 45 | |||
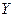 (т/сут.) (т/сут.)
|  (шт.) (шт.)
|  (м3/сут.) (м3/сут.)
| 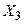 (шт.) (шт.)
|
| 3,5 | |||
| 3,5 | |||
| 3,6 | |||
| 3,6 | |||
| 3,5 | |||
| 3,5 | |||
| 3,4 | |||
| 3,3 | |||
| 3,4 | |||
| 3,3 | |||
| 3,2 | |||
| 3,2 | |||
| 3,1 | |||
| 3,2 | |||
| 3,1 | |||
| 3,1 | |||
| 3,0 | |||
| 3,1 | |||
| 3,0 | |||
| 3,0 |
Вариант №12.
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи жидкости с начала разработки ( ), от годовой добычи жидкости из перешедших скважин (
), от годовой добычи жидкости из перешедших скважин ( ), среднегодовой обводненности (
), среднегодовой обводненности ( ) и от среднего дебита действующих скважин по жидкости (
) и от среднего дебита действующих скважин по жидкости (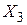 ) приведены в табл. 46.
) приведены в табл. 46.
| Таблица 46 | |||
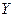 (тыс. т) (тыс. т)
|  (тыс. т) (тыс. т)
|  (%) (%)
| 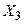 (т/сут.) (т/сут.)
|
| 34,5 | 2,8 | 3,9 | |
| 34,4 | 2,8 | ||
| 34,3 | 2,7 | ||
| 34,2 | 2,6 | 4,1 | |
| 34,1 | 2,5 | 4,1 | |
| 2,4 | 4,1 | ||
| 33,8 | 2,4 | 4,3 | |
| 33,7 | 2,3 | 4,3 | |
| 33,6 | 2,2 | 4,2 | |
| 33,4 | 2,2 | 4,4 | |
| 33,2 | 2,1 | 4,4 | |
| 33,1 | 2,0 | 4,6 | |
| 32,9 | 2,0 | 4,5 | |
| 32,7 | 1,9 | 4,7 | |
| 32,5 | 1,8 | 4,7 |
Вариант №13
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи нефти с начала разработки ( ), от суммарной добычи нефти из скважин предыдущего года (
), от суммарной добычи нефти из скважин предыдущего года ( ), падение добычи нефти (
), падение добычи нефти ( ) и фонда добывающих скважин на конец года (
) и фонда добывающих скважин на конец года (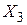 ) приведены в табл. 47.
) приведены в табл. 47.
| Таблица 47 | |||
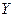 (тыс.т) (тыс.т)
|  (тыс.т) (тыс.т)
|  (тыс.т) (тыс.т)
| 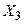 (шт.) (шт.)
|
| 100,5 | 30,4 | -0,5 | |
| -0,9 | |||
| 133,1 | 32,1 | -1 | |
| 163,1 | 31,1 | -0,9 | |
| 192,6 | 30,2 | -0,9 | |
| 220,9 | 29,3 | -0,9 | |
| 248,5 | 28,4 | -0,9 | |
| 275,1 | 27,5 | -0,8 | |
| 26,7 | -0,8 | ||
| 326,1 | 25,9 | -0,8 | |
| 350,4 | 25,1 | -0,7 | |
| 24,3 | -0,7 | ||
| 379,5 | 23,6 | -0,6 |
Вариант №14
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи нефти с начала разработки ( ), от суммарной добычи нефти из скважин предыдущего года (
), от суммарной добычи нефти из скважин предыдущего года ( ), падение добычи нефти (
), падение добычи нефти ( ) и коэффициента нефтеизвлечения (
) и коэффициента нефтеизвлечения (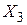 ) приведены в табл. 48.
) приведены в табл. 48.
| Таблица 48 | |||
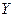 (тыс.т) (тыс.т)
|  (тыс. т) (тыс. т)
|  (тыс.т) (тыс.т)
| 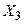 (%) (%)
|
| -0,7 | 0,9 | ||
| 22,7 | -0,9 | 1,2 | |
| 86,9 | 31,7 | -0,9 | 1,9 |
| 117,3 | 31,2 | -0,8 | 2,5 |
| 147,1 | 30,5 | -0,8 | 3,2 |
| 176,1 | 29,7 | -0,8 | 3,8 |
| 204,5 | -0,7 | 4,4 | |
| 232,2 | 28,4 | -0,7 | 5,0 |
| 259,2 | 27,7 | -0,6 | 5,6 |
| 285,6 | 26,4 | -0,6 | 6,2 |
| 311,4 | 25,8 | -0,6 | 6,7 |
| 336,6 | 25,2 | -0,5 | 7,3 |
| 361,2 | 24,6 | -0,5 | 7,8 |
| 385,3 | -0,5 | 8,3 | |
| 408,7 | 23,5 | -0,5 | 8,8 |
Вариант №15
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи жидкости с начала разработки ( ), от годовой добычи жидкости из перешедших скважин (
), от годовой добычи жидкости из перешедших скважин ( ), среднегодовой обводненности (
), среднегодовой обводненности ( ) и от среднего дебита действующих скважин по жидкости (
) и от среднего дебита действующих скважин по жидкости (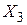 ) приведены в табл. 49.
) приведены в табл. 49.
| Таблица 49 | |||
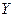 (тыс.т) (тыс.т)
|  (тыс. т) (тыс. т)
|  (%) (%)
| 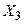 (т/сут.) (т/сут.)
|
| 32,7 | 4,8 | 2,7 | |
| 32,7 | 6,8 | 2,8 | |
| 32,6 | 8,8 | 2,8 | |
| 32,5 | 10,7 | 2,8 | |
| 32,4 | 12,6 | 2,9 | |
| 32,5 | 14,4 | 2,9 | |
| 32,3 | 16,2 | 3,0 | |
| 32,2 | 17,9 | 3,0 | |
| 32,1 | 19,5 | 2,9 | |
| 21,2 | 3,0 | ||
| 31,8 | 22,8 | 3,0 | |
| 31,7 | 24,3 | 3,1 | |
| 31,6 | 25,8 | 3,1 | |
| 31,5 | 27,2 | 3,2 | |
| 31,4 | 28,7 | 3,2 |
Вариант №16.
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость среднего дебита действующих скважин по нефти ( ), от фонда действующих нагнетательных скважин на конец года (
), от фонда действующих нагнетательных скважин на конец года ( ), средней приемистости нагнетательных скважин (
), средней приемистости нагнетательных скважин ( ) и темпа отбора от начальных извлекаемых запасов (
) и темпа отбора от начальных извлекаемых запасов (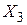 ) приведены в табл. 50.
) приведены в табл. 50.
| Таблица 50 | |||
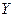 (т/сут.) (т/сут.)
|  (шт.) (шт.)
|  (м3/сут.) (м3/сут.)
| 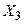 (%) (%)
|
| 2,5 | |||
| 2,7 | |||
| 2,6 | 2,3 | ||
| 2,7 | 2,2 | ||
| 2,6 | 2,1 | ||
| 2,6 | 2,2 | ||
| 2,5 | 2,1 | ||
| 2,5 | |||
| 2,5 | 2,1 | ||
| 2,5 | 1,9 | ||
| 2,4 | 1,9 | ||
| 2,4 | 1,8 | ||
| 2,4 | 1,8 | ||
| 2,3 | 1,7 | ||
| 2,3 | 1,7 | ||
| 2,3 | 1,9 | ||
| 2,2 | 2,3 | ||
| 2,3 | 1,9 | ||
| 2,3 | 2,1 | ||
| 2,2 |
Вариант №17
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи нефти с начала разработки ( ), от коэффициента нефтеизвлечения (
), от коэффициента нефтеизвлечения ( ), темпа отбора от начальных извлекаемых запасов (
), темпа отбора от начальных извлекаемых запасов ( ) и среднего дебита действующих скважин по нефти (
) и среднего дебита действующих скважин по нефти (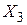 ) приведены в табл. 51.
) приведены в табл. 51.
| Таблица 51 | |||
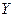 (тыс.т) (тыс.т)
|  (%) (%)
|  (%) (%)
| 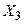 (т/сут.) (т/сут.)
|
| 1,5 | 2,8 | 3,6 | |
| 133,1 | 1,9 | 2,8 | 3,6 |
| 163,3 | 2,4 | 2,7 | 3,5 |
| 192,6 | 2,8 | 2,6 | 3,5 |
| 220,9 | 3,2 | 2,5 | 3,4 |
| 275,1 | 2,4 | 3,4 | |
| 4,4 | 2,4 | 3,3 | |
| 326,1 | 4,8 | 2,3 | 3,2 |
| 350,4 | 5,1 | 2,2 | 3,2 |
| 5,5 | 2,2 | 3,1 | |
| 396,9 | 5,8 | 2,1 | 3,2 |
| 419,9 | 6,1 | 3,1 | |
| 440,6 | 6,4 | 3,1 | |
| 461,5 | 6,7 | 1,9 | |
| 481,7 | 1,8 | 3,1 |
Вариант №18
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость добычи жидкости сначала разработки ( ), от закачки агента за год (
), от закачки агента за год ( ), закачки агента с начала разработки (
), закачки агента с начала разработки ( ) и среднего дебита действующих скважин по жидкости (
) и среднего дебита действующих скважин по жидкости (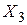 ) приведены в табл. 52.
) приведены в табл. 52.
| Таблица 52 | |||
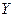 (тыс. т) (тыс. т)
|  (тыс. т/год) (тыс. т/год)
|  (тыс. т) (тыс. т)
| 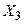 (т/сут.) (т/сут.)
|
| 44,5 | 2,8 | ||
| 44,3 | 2,8 | ||
| 2,8 | |||
| 43,7 | 2,9 | ||
| 43,4 | 2,9 | ||
| 43,1 | |||
| 42,8 | |||
| 42,5 | 2,9 | ||
| 42,3 | |||
| 41,7 | 3,1 | ||
| 41,4 | 3,1 | ||
| 41,4 | 3,2 | ||
| 40,8 | 3,2 | ||
| 40,5 | 3,3 |
Вариант №19
Прогнозные показатели разработки по нефти на одном из месторождений Тюменской области, характеризующие зависимость суммарной добычи нефти из скважин предыдущего года ( ), от падения добычи нефти (
), от падения добычи нефти ( ), процента падения добычи нефти (
), процента падения добычи нефти ( ) и фонда добывающих скважин на конец года (
) и фонда добывающих скважин на конец года (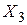 ) приведены в табл. 53.
) приведены в табл. 53.
| Таблица 53 | |||
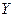 (тыс. т) (тыс. т)
|  (тыс. т) (тыс. т)
|  (%) (%)
| 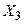 (шт.) (шт.)
|
| -1,1 | -2,4 | ||
| -0,9 | -2,6 | ||
| 32,1 | -1 | -2,6 | |
| 31,1 | -0,9 | -2,6 | |
| 29,3 | -0,9 | -2,7 | |
| 28,4 | -0,9 | -2,7 | |
| 27,5 | -0,8 | -2,7 | |
| 25,9 | -0,8 | -2,8 | |
| 24,3 | -0,7 | -2,8 | |
| 22,9 | -0,7 | -2,8 | |
| 21,5 | -0,7 | -2,9 | |
| 20,2 | -0,6 | -2,9 | |
| -0,5 | -3,1 |
Вариант №20
Исходные данные по цеху акционерного объединения машиностроительного профиля за 10 месяцев, характеризующие зависимость между себестоимостью произведенной продукции ( ), стоимостью материалов (
), стоимостью материалов ( ), основной зарплатой (
), основной зарплатой ( ) и расходами по содержанию и эксплуатации оборудования (
) и расходами по содержанию и эксплуатации оборудования (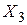 ) представлены в табл. 54.
) представлены в табл. 54.
| Таблица 54 | |||
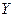 (тыс. руб.) (тыс. руб.)
|  (тыс. руб.) (тыс. руб.)
|  (тыс. руб.) (тыс. руб.)
| 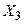 (тыс. руб.) (тыс. руб.)
|
| 82,3 | 36,4 | 11,5 | 14,2 |
| 83,8 | 36,6 | 11,5 | 13,9 |
| 81,5 | 37,9 | 11,6 | 15,2 |
| 83,1 | 38,2 | 11,8 | 16,5 |
| 84,3 | 39,4 | 16,7 | |
| 82,6 | 39,8 | 12,2 | 17,2 |
| 85,4 | 40,1 | 12,5 | 18,3 |
| 84,6 | 41,5 | 12,6 | 18,6 |
| 86,8 | 42,6 | 12,8 | 19,4 |
| 88,3 | 45,7 | 13,2 | 20,7 |
Вариант №21
Исходные данные по цеху акционерного объединения машиностроительного профиля за 10 месяцев, характеризующие зависимость между себестоимостью произведённой продукции ( ), стоимостью материалов
), стоимостью материалов  , основной зарплатой (
, основной зарплатой ( ) и цеховыми расходами (
) и цеховыми расходами (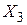 ) предоставлены в табл. 55.
) предоставлены в табл. 55.
| Таблица 55 | |||
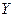 (тыс. руб.) (тыс. руб.)
|  (тыс. руб.) (тыс. руб.)
|  (тыс. руб.) (тыс. руб.)
| 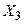 (тыс. руб.) (тыс. руб.)
|
| 81,5 | 37,9 | 11,6 | 9,5 |
| 82,3 | 36,5 | 11,5 | 10,6 |
| 83,8 | 36,6 | 11,5 | 7,8 |
| 83,1 | 38,2 | 11,8 | 9,1 |
| 84,3 | 39,4 | 13,6 | |
| 82,6 | 39,8 | 12,2 | 14,1 |
| 85,4 | 40,1 | 12,5 | 14,6 |
| 84,6 | 41,5 | 12,6 | 15,1 |
| 86,8 | 42,6 | 12,8 | |
| 88,3 | 45,7 | 13,2 | 17,2 |
Вариант №22
Имеются данные, характеризующие зависимость нормы расхода моторного масла ( ) на угар и замену марки
) на угар и замену марки  от максимальной мощности двигателя (
от максимальной мощности двигателя ( ), максимального крутящего момента (
), максимального крутящего момента ( ), линейной нормы расхода топлива (
), линейной нормы расхода топлива (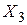 ), и скорости автомобиля (
), и скорости автомобиля ( ) (табл. 56).
) (табл. 56).
| Таблица 56 | ||||
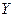 (л/100 л. т) (л/100 л. т)
|  (л. с) (л. с)
| 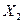 () ()
|  (л) (л)
|  (км/ч) (км/ч)
|
| 1,3 | 7,4 | |||
| 1,3 | 7,6 | |||
| 0,8 | 8,2 | |||
| 1,3 | 8,2 | |||
| 2,2 | 20,5 | 21,5 | ||
| 2,2 | ||||
| 1,8 | 73,5 | 10,8 | ||
| 2,2 | ||||
| 22,8 | ||||
| 2,1 | ||||
| 2,2 | 17,5 | |||
| 2,3 | ||||
| 1,8 | 18,4 | |||
| 2,8 | ||||
| 2,2 | ||||
| 2,1 | ||||
| 2,1 | ||||
| 47,3 | ||||
| 1,8 |
Вариант №23
Имеются данные, характеризующие зависимость нормы расхода моторного масла ( ) на угар и замену марки
) на угар и замену марки  от максимальной мощности двигателя (
от максимальной мощности двигателя ( ), линейной нормы расхода топлива (
), линейной нормы расхода топлива ( ), скорости двигателя (
), скорости двигателя (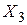 ) и контрольного расхода топлива при данной скорости (
) и контрольного расхода топлива при данной скорости ( ) (табл. 57).
) (табл. 57).
| Таблица 57 | ||||
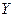 (л/100 л. т.) (л/100 л. т.)
|  (л. с.) (л. с.)
|  (л) (л)
| 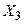 (км/ч) (км/ч)
|  (л) (л)
|
| 1,3 | ||||
| 1,3 | ||||
| 0,8 | 9,45 | |||
| 1,3 | 8,85 | |||
| 2,2 | 21,5 | |||
| 2,2 | ||||
| 1,8 | 73,5 | 9,3 | ||
| 2,2 | 10,6 | |||
| 22,8 | ||||
| 2,1 | ||||
| 2,2 | 13,1 | |||
| 2,3 | 10,6 | |||
| 1,8 | 11,8 | |||
| 2,8 | 38,5 | |||
| 2,2 | ||||
| 2,1 | ||||
| 2,1 | ||||
| 35,9 | ||||
| 1,8 |
Вариант №24
Имеются данные, характеризующие зависимость нормы расхода моторного масла  на угар и замену марки
на угар и замену марки  от максимальной мощности двигателя (
от максимальной мощности двигателя ( ), диаметра цилиндра (
), диаметра цилиндра ( ), линейной нормы расхода топлива (
), линейной нормы расхода топлива (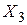 ) и скорости (
) и скорости ( ) (табл. 58).
) (табл. 58).
Дата добавления: 2015-10-29; просмотров: 181 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Измерение тесноты связи множественной линейной регрессии | | | LOPČYK, ŠČO VYŽYW |