Колебательная переходная характеристика.

Колебательная переходная характеристика (рис.14.3) описывается колебательным звеном с передаточной функцией (14.4).

, (14.5)

где - коэффициент демпфирования, численное значение которого лежит в пределах .

Дифференциальное уравнение колебательного звена, которое отвечает передаточной функции (14.5), имеет вид:

(14.6)

Рис.14.3. Определение параметров передаточной функции колебательного звена по трем точкам

Поскольку , то корни характеристического уравнения будут комплексными:

,

где - логарифмический декремент затухания;

- частота колебаний.

Решение дифференциального уравнения колебательного звена имеет вид:

, (14.7)

где - степень колебательности.

Искомые динамические параметры определяют из переходной характеристики (рис.14.3) по формулам:

, (14.8)

. (14.9)

Пример 14.1. Рассмотрим таблично заданную переходную функцию колебательного процесса. График функции показан на рис.14.4.

Таблица 14.1

Данные переходной функции колебательного процесса

, c		, c		, c		, c		, c
1	0.205	6	1.213	11	0.945	16	1.014	21	0.997
2	0.629	7	1.080	12	0.985	17	1.002	22	1.000
3	1.026	8	0.969	13	1.016	18	0.994	23	1.002
4	1.257	9	0.913	14	1.028	19	0.991	24	1.002
5	1.300	10	0.912	15	1.025	20	0.993	25	1.003

Найдем параметры передаточной функции колебательного звена

.

Учитывая, что процесс колебательный, то значение коэффициента демпфирования находится в диапазоне и корни характеристического уравнения комплексные.

Динамические параметры передаточной функции колебательного звена находим по выражениям:

;

,

где , - точки сечения линии установившегося значения переходной функцией.

Решение дифференциального уравнения колебательного звена имеет вид:

,

где и из корней характеристического уравнения:

.

- степень колебательности.

Воспроизведенная переходная функция приведена на рис.14.4.

Рис.14.4. Заданный и воспроизведенный колебательные процессы

Относительная погрешность воспроизведенной функции в точке составляет 3,16%, в точке - 2,6%.

При анализе динамических процессов в системах электропривода дифференциальное уравнение колебательного процесса записывают в виде:

. (14.10)

Введем к рассмотрению динамические параметры и , что однозначно связанные с и такими выражениями:

- угловая частота недемпфированных колебаний, которые определяют масштаб времени процесса ;

- относительный коэффициент затухания колебаний, которое определяет колебательность процесса .

Из этих соотношений можно получить:

, (14.11)

. (14.12)

Рис.14.5. К определению параметров передаточной функции колебательного звена

Вся область изменения может быть разбита на три интервала: ; ; .

В первом интервале кривая разгона (рис.14.5.) будет резко колебательной () и по величине перерегулирования может быть определенная величина :

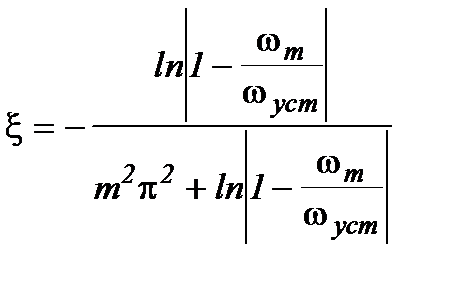(14.13),

где - порядковый номер экстремума, - ордината графика в точке экстремума.

Угловая частота колебаний определяется из выражения

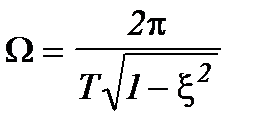, (14.14)

где - период колебаний.

Пример 14.2. Рассмотрим таблично заданную переходную функцию колебательного процесса. График функции показан на рис.14.6.

Таблица 14.2.

Данные переходной функции колебательного процесса

, c		, c		, c		, c		, c
1	0.205	6	1.213	11	0.945	16	1.014	21	0.997
2	0.629	7	1.080	12	0.985	17	1.002	22	1.000
3	1.026	8	0.969	13	1.016	18	0.994	23	1.002
4	1.257	9	0.913	14	1.028	19	0.991	24	1.002
5	1.300	10	0.912	15	1.025	20	0.993	25	1.003

Найдем параметры передаточной функции колебательного звена представленной в виде:

.

Динамические параметры звена найдем на первом полупериоде колебаний. Для этого промежутка: порядковый номер экстремума , относительная величина перерегулирования

.

Параметр определим как

.

Период колебаний

.

Угловая частота колебаний

.

Постоянные времени передаточной функции

;

.

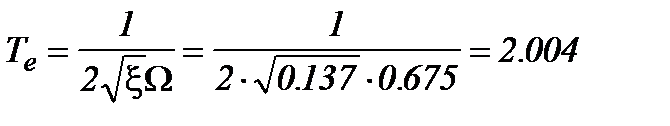Воспроизведенная переходная функция приведена на рис.14.6.

Рисунок 14.6 - Заданный и воспроизведенный колебательные процессы

№	y(x)	x'	y'	b0	b1
		x	y	b0`	b1`
		x	1/y	b0`	b1`
		1/x	y	b0`	b1`
		x	x/y	b0`	b1`
		x	lg y	10^b0`	10b1`
		x	ln x	exp(b0`)	b1`
		x	lg y	10^b0`	b1`
				1/y	b1`
		lg x	lg y	10^b0`	b1`
		lg x	y	b0`	b1`
		ln x	y	b0`	b1`
		x	1/y	1/b1`	b0`/b1`
		1/x	1/y	1/b1`	b0`/b1`
		1/x	lg y	10^b0`	b1`
		x^n	y	b0`	b1`

Дата добавления: 2015-10-29