Жалпы түсініктер және анықтамасы

Кез келген группалық код (n, k) матрица түрінде жазылуы мүмкін, қосылатын k сызықты тәуелсіз жолдар n символдар және керісінше, кез келген қасиеті k сызықты тәуелсіз n-разрядты кодтың комбинациясы кейбір топтық кодты құраушы матрица түрінде қарастырылуы мүмкін.Көп түрлі осындай кодтар арасынан айналымның қосымша шартымен байланысқан туындатушы матрицалар жолдарының кодтарын ерекшелеуге болады.

Бір комбинацияны циклдық қозғалу арқылы туындатушы матрицалардың барлық жолдарын алуға болады, бұл кодты туындатушы деп аталады. Бұл шартты қанағаттандыратын кодтар циклдық кодтар деген атқа ие болған.

Қозғалыс оңнан солға қарай жүргізіледі және сол жақ шеттегі символ комбинацияның соңына орналастырылады.Жазайық, мысал, комбинациялар кодтарының қасиеті, циклдық қозғалатын комбинациялар арқылы алынған түрі 001011:

Циклдық мүмкін (n,k)-кодтардың саны әртүрлі топтық (n,k)-кодтар санынан көп есе аз болады.

Циклдық кодтарды суреттегенде n-разрядты комбинациялық кодтар көпмүшелі фиктивті х-айнымалы түрінде көрсетіледі. у және х дәрежелері разрядтар нөмірлеріне сәйкес келеді (нөлден бастап),ал жалпы жағдайда коэффиценті х деп GF(q) өрісінің элементі болып табылады. х⁰ = 1 фиктивті айнымалысы ең төменгі санның разрядына сәйкес келеді. GF(q) өрісінің к өпмүше коэффицентін GF(q) өрісінің үстіндегі көрмүшесі деп атайды. Екілік кодтарды қарастырмауымызға байланысты, х -тің коэффиценті тек 0 және 1 сандары болады. Басқаша айтқанда, GF(2) өріс үстінде көпмүшені оперировать етеміз. Жазып алайық, мысал, 01011 кодтық комбинацияны құраушы көпмүше түрінде:

G(x) = 0·x⁴ + 1·x³ + 0·x² + 1·x + 1

Нөлдік коэффицентті жазғанда көпмүшелік түседі, туындатушы көпмүшелік:

G(x) = x³ + x + 1

Нөлдік коэффицентпен қосылатын х- тің үлкен дәрежесін көпмүшеліктің дәрежесі деп атаймыз. Енді кодтық комбинацияларға жасалған әрекеттер көпмүшеліктерге әрекетке өтеді. Көпмүшеліктерді қосу коэффиценттерді екінші модуль арқылы жүзеге асырады.

Көрсетілген циклдық қозғалыс кейбір туындатушы көпмүшенің дәрежесін n – k деп бірлікті кодтық комбинацияның соңына ауыстырмай х-ке көбейту сияқты қарапайым орындайды. Көбейтеміз, мысал, матрицаның бірінші жолы (001011), g₀(х) = x³ + x + 1 сәйкес көпмүшені, х-ке, матрицаның екінші жолын (010110), сәйкесінше көпмүшені х • g₀(x) аламыз.

Мына екі комбинацияның қосындысы x³ + x + 1 және х+1арқылы табылған мәні кодтық комбинацияның шыққан мәніне тең екеніне көз жеткіземіз. Шынымен де,

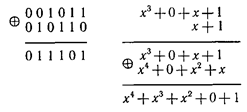
Циклдық қозғалыс жолдар матрица бірлігімен үлкен (n-м) разрядында (солдан) тең болады көпмүшенің х жолына сәйкес болатын, біруақытты алыну көпмүшенің нәтижесіне теңхⁿ + 1= хⁿ– 1 модуль бойынша хⁿ + 1.

Бұл жерде циклдық кодтың кез келген рұқсат етілген комбинациясы модуль xⁿ + l бойынша құралатын көпмүшенің басқа бір көпмүшеге көбейтілуінің нәтижесінен алынады.Басқаша айтсақ,дәл келетін таңдауда құралатын көпмүше және циклдық кодтың кез келген көпмүшесі қалдықсыз бөлінетін болады.Рұқсат етілмеген кодтық комбинациясына сәйкес келетін,бірде бір көпмүше,құралатын көпмүше қалдықсыз бөлінбейді.Бұл қасиет қатені табуға мүмкіндік береді.Көпмүшенің көбеюі және бөлінуі кері байланыс бар жылжу регистрында оңай орындалады.

Дата добавления: 2015-10-23