Зведення сил інерції точок тіла до головного вектора

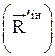та головного моменту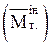

За центр зведення візьмемо початок координат – точку А. Через те, що нам прийдеться рівняння (1) і (2) проєціювати на осі координат, отримаємо проекції головного вектора і головного моменту на осі координат Ахуz.

Згадаємо, чому дорівнюють головний вектор і головний момент системи n сил (теорема Пуансо з статики) 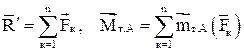; якщо це сили інерції, то звичайно

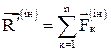. (3)

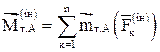. (4)

“Розіб’ємо” тіло на точки, маса кожної m_к, координати т.М (х_к, у_к, z_к) (рисунок 2,а). Покажемо складові Д’Аламебрових сил інерції точки М нормальну та дотичну за назвою пришвидшень точки М при обертальному русі тіла, на рис. 2,б (вид зверху перерізу тіла, в якому знаходиться точка М). Нормальна (або відцентрова) сила інерції дорівнює 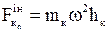, спрямована протилежно нормальному пришвидшенню. Дотична (або обертальна) сила інерції дорівнює 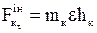, спрямована перпендикулярно до нормальної проти кутового пришвидшення ε. Знайдемо складові цих двох сил інерції вздовж 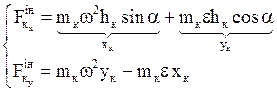осей Ах і Ау

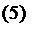
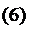
Тоді, враховуючи (3), маємо проекції головного вектора на осі координат

.

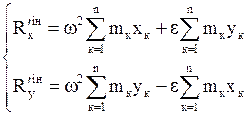Як відомо (див. тему 2), ,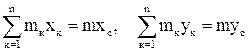

де х_с, у_с –координати центру мас. Тому маємо:

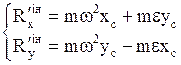. (7)

Сили інерції усіх точок тіла лежать в площинах, перпендикулярних до осі z, тому 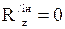. Проекції головного моменту сил інерції на осі координат отримаємо як суми моментів сил інерції точок тіла відносно осей координат (згадаємо з розділу “Статика” ). Для цього прикладемо 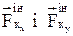до точки М на рисунку 2,а. Маємо

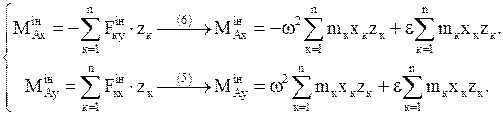
(Що це за величини 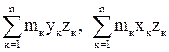? Відцентрові моменти інерції 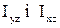, відповідно).

Маємо проекції головного моменту сил інерції на осі координат Ах і Ау

. (8)

Навколо осі z моменти створюють тільки дотичні складові сил інерції точок, тому

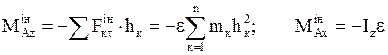. (9)

Що це за сума 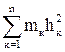? Осьовий момент інерції тіла відносно осі z. .

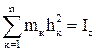На рисунку ми не будемо показувати головний вектор і головний момент сил інерції, пам’ятаючи що нам відомі, їхні проекції на осі координат , .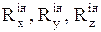

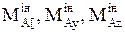Оскільки вже маємо схему сил, можна перейти до складання рівнянь умовної рівноваги тіла під дією довільної просторової системи сил. З розділу “Статика” згадайте: скільки рівнянь рівноваги треба скласти для довільної просторової системи сил? Шість.

Дата добавления: 2015-10-29