Обертається навколо нерухомої осі

Умови відсутності динамічних реакцій означають, що Ставимо умову

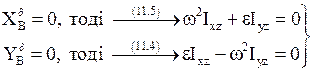(12)

Через те, що визначник системи рівнянь (12) 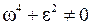, маємо розв’язок системи (12) , тобто вісь А_z – головна вісь. Далі:

(13)

З тієї ж причини (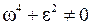), розв’язок системи рівнянь (13) 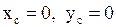тобто вісь обертання проходить через центр мас. Умови

(14)

означають, що вісь обертання є головною центральною, її ще називають вільною, бо вона вільна від динамічних реакцій. Якщо тільки 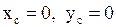, а - цей випадок називають статичною зрівноваженістю тіла обертання. В цьому випадку тобто 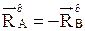, реакції опор в точках А і В утворюють пару сил. У випадку виконання умов (14) маємо динамічну зрівноваженість.

Статичної зрівноваженості буває досить для шківів, махових коліс. Якщо вал довгий і на ньому декілька мас, треба займатись балансуванням. Цьому вас будуть навчати в курсі “Теорія механізмів і машин”.

Загальний прийом балансування: вирізають частинку тіла там, де воно важче, або там де легше дірочку заливають більш важким металом (наприклад свинцем).

Зауваження.

1) Формули (7) і (8) отримані без вимог до осей координат, тобто осі можуть бути нерухомі, або рухомі, зв’язані з тілом. Краще брати рухомі, тоді моменти інерції будуть постійними величинами.

2) Знайдені з рівнянь (11) динамічні реакції відносно рухомих осей координат будуть рухатись разом з осями Ах і Ау. Це означає, що на опори будуть діяти сили, які змінюються за напрямком, що приводить до розхитування опор та до їх руйнування.

Висновок. Обов’язково треба враховувати сили інерції в швидкохідних і важких машинах; якщо якась ланка машини має пришвидшення (а при обертальному русі навіть рівномірному, точки завжди мають пришвидшення), треба зробити її легшою.

Для самостійного висновку. Пропонується три випадки валу, що обертається, з ексцентрично насаженими масами (рисунок 3).

Питання.

1) В якому з цих випадків не виникають динамічні реакції в опорах А і В?

2) Чи є тут випадки статичної зрівноваженості? динамічної зрівноваженості валу?

Дата добавления: 2015-10-29