
Читайте также:
|
вариантов текущего контроля
Домашнее задание №1 «Элементарные функции и их графики»
Задача 1. Найти область определения функции  .
.
Задача 2. Исследовать функцию  на четность (нечетность).
на четность (нечетность).
Задача 3. Используя элементарные преобразования, построить эскизы графиков следующих функций:
а)  , б),
, б), 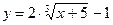 в)
в)  ,
,
г)  , д)
, д) 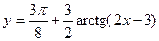 .
.
Задача 4. Построить эскиз графика рациональной функции 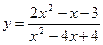 , исследуя его расположение относительно оси абсцисс и асимптот.
, исследуя его расположение относительно оси абсцисс и асимптот.
Задача 5. Используя правила построения графика суммы, произведения, частного или композиции двух функций, построить эскиз графика функции  .
.
Домашнее задание №2 «Пределы и непрерывность»
Задача 1. Для заданной последовательности  и числа
и числа 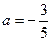 доказать, что
доказать, что  , определив для каждого
, определив для каждого 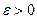 число
число  , такое, что
, такое, что 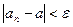 для всех
для всех  . Заполнить таблицу:
. Заполнить таблицу:

| 0,1 | 0,01 | 0,001 |

|
Задача 2. Вычислить следующие пределы:
а)  ; б)
; б)  ; в)
; в) 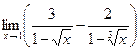 ;
;
г)  ; д)
; д) 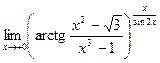 ; е)
; е) 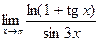 .
.
Задача 3.
1) Показать, что данные функции f и g являются бесконечно малыми или бесконечно большими при указанном стремлении аргумента.
2) Для каждой функции f и g записать главную часть (эквивалентную ей функцию) вида 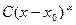 при
при 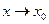 , или
, или  при
при  , указать их порядки малости (роста).
, указать их порядки малости (роста).
3) Сравнить f и g при 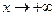 , если
, если  ,
,  .
.
Задача 4. Найти точки разрыва функции 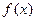 и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:
и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:

Домашнее задание №3 «Исследование функций и построение графиков»
Задача 1. Исследовать заданные функции и построить их графики:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 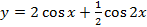 .
.
Задача 2. Разложить функцию 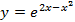 по формуле Маклорена 3-го порядка с остаточным членом в форме Пеано.
по формуле Маклорена 3-го порядка с остаточным членом в форме Пеано.
Задача 3. Из всех равнобедренных треугольников с заданным периметром найти тот, у которого площадь максимальна.
Контрольная работа «Техника дифференцирования»
Задача 1. Для заданных функций найти  .
.
1.  . 2.
. 2.  . 3.
. 3. 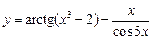 .
.
4. 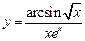 . 5.
. 5. 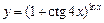 . 6.
. 6. 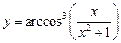
Задача 2. Найти производную  функции
функции 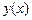 , заданной параметрически:
, заданной параметрически:

Задача 3. Найти производные 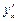 ,
,  в точке
в точке  функции
функции 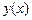 , заданной неявно уравнением
, заданной неявно уравнением 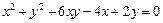 .
.
Задача 4. Составить уравнение касательной и нормали к кривой  ,
,  в точке
в точке  . Сделать чертеж.
. Сделать чертеж.
Задача 5. Вывести, исходя из определения, производную функции 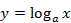 .
.
Замечание: возможно включение теоретических вопросов.
Дата добавления: 2015-10-29; просмотров: 119 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модуль 1. Элементарные функции и пределы | | | Модуль 2 Дифференциальное исчисление функций одного переменного |