
Читайте также:
|
Явище удару для тіла, яке обертається навколо нерухомої осі виникає досить часто:
– при несподіваних зупинках;
– при зміні тиску на поршень двигуна внутрішнього згорання;
– при випробуваннях на міцність тіла за допомогою ударних машин;
– в балістичних маятниках і ін.
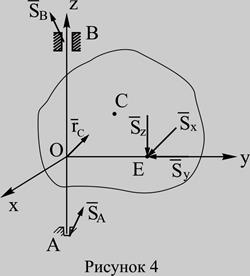
Постановка задачі. Маємо тіло відомої форми, масою m, яке обертається з кутовою швидкістю  навколо нерухомої осі. В деякий момент часу тіло зазнає дії зовнішнього ударного імпульсу
навколо нерухомої осі. В деякий момент часу тіло зазнає дії зовнішнього ударного імпульсу  тривалістю τ сек.. Позначимо: після удару кутову швидкість тіла
тривалістю τ сек.. Позначимо: після удару кутову швидкість тіла  ; точку, в якій прикладений імпульс
; точку, в якій прикладений імпульс  точка Е (рисунок 4). Як відомо, при ударі дією неударних сил нехтуємо. Розглянемо випадок, коли вісь обертання не проходить через точку С
точка Е (рисунок 4). Як відомо, при ударі дією неударних сил нехтуємо. Розглянемо випадок, коли вісь обертання не проходить через точку С  . Під час удару в опорах А і В виникнуть імпульси реакцій
. Під час удару в опорах А і В виникнуть імпульси реакцій  . (Згадаємо, що є мірою взаємодії тіл при ударі? – Імпульс сили, а не сила).
. (Згадаємо, що є мірою взаємодії тіл при ударі? – Імпульс сили, а не сила).
 Мета: визначити умови, при яких імпульси в опорах дорівнюють нулеві.
Мета: визначити умови, при яких імпульси в опорах дорівнюють нулеві.
Виберемо осі координат: z – вісь обертання, у – проведемо через точку Е (рисунок 4). Щоб визначити імпульси реакцій в опорах, скористаємось загальними теоремами динаміки. Згадаємо, які теореми застосовуються в теорії удару (див. тему 3, тему 4)
– Теорема імпульсів
– Теорема про зміну кінетичного моменту.
В нашому випадку маємо ці теореми
 (15)
(15)
 , (16)
, (16)
де  - кількість руху тіла після удару і до удару, відповідно
- кількість руху тіла після удару і до удару, відповідно  - момент кількості руху тіла відносно точки О після удару та до удару, відповідно.
- момент кількості руху тіла відносно точки О після удару та до удару, відповідно.
Спроеціювавши (15) і (16) на осі координат, можна отримати рівняння для визначення імпульсів в опорах  . Цього ми робити не будемо, а поставимо умову відсутності опорних імпульсів:
. Цього ми робити не будемо, а поставимо умову відсутності опорних імпульсів:  . Згадаємо (тема 3), чому дорівнює кількість руху тіла
. Згадаємо (тема 3), чому дорівнює кількість руху тіла  . Визначимо проекції кількості руху на осі координат
. Визначимо проекції кількості руху на осі координат  ,
,  ,
,  , (бо
, (бо  лежить в площині, перпендикулярній до осі Оz). Проекції швидкості точки С на осі координат знайдемо за формулою Ейлера, розкривши визначник
лежить в площині, перпендикулярній до осі Оz). Проекції швидкості точки С на осі координат знайдемо за формулою Ейлера, розкривши визначник
 .
.
Тобто, маємо  (17)
(17)
Згадаємо (тема 4), чому дорівнюють кінетичні моменти відносно осей координат тіла, що обертається навколо нерухомої осі Оz з кутовою швидкістю:
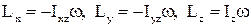 . (18)
. (18)
Проекції (15) і (16) на осі координат, з врахуванням (17) і (18) і того, що імпульси в опорах дорівнюють нулеві мають вигляд:
 (19)
(19)
В цих рівняннях відсутні опорні імпульси  , тобто це є умови, при яких імпульси в опорах не виникають. Розглянемо висновки з цих рівнянь.
, тобто це є умови, при яких імпульси в опорах не виникають. Розглянемо висновки з цих рівнянь.
1) З (19.3), (19.4), (19.5) слідує, що  , тобто ударний імпульс повинний лежати в горизонтальній площині, а вісь Оz – головна вісь.
, тобто ударний імпульс повинний лежати в горизонтальній площині, а вісь Оz – головна вісь.
2) Якщо домножити (19.1) на хС, а (19.2) на уС і скласти результати, отримаємо  , тобто скалярний добуток вектора
, тобто скалярний добуток вектора  і радіуса-вектора точки С дорівнює нулеві
і радіуса-вектора точки С дорівнює нулеві  , значить кут між
, значить кут між  дорівнює 90 º.
дорівнює 90 º.
3) Щоб визначити відстань ОЕ треба поділити (19.6) на (19.1)
 . (20)
. (20)
Висновок. Умови відсутності імпульсів в опорах А і В:
1) Площина Оху, в якій повинний лежати ударний імпульс, перетинається з віссю z в точці О, для якої ця вісь є головною.
2) Лінія дії ударного імпульсу перпендикулярна до площини, в якій лежать вісь обертання і центр мас тіла.
3) Ударний імпульс треба прикласти в точці Е, положення якої визначається формулою (20). Точка Е зветься центром удару.
Зауваження
1) Якщо тіло має площину матеріальної симетрії, яка перпендикулярна осі обертання (що на практиці буває досить часто), тоді вісь z – завжди головна в точці О.
2) Існує зв’язок між радіусом інерції тіла відносно осі z і центром удару. Покажемо площину матеріальної симетрії на рисунку 5. Згідно з (20) маємо

 , тоді
, тоді  (21)
(21)
До речі, центр удару і центр хитань фізичного маятника – це одна й та сама точка.
3) Якщо вісь обертання проходить через центр мас (уС = 0 в формулі (20)), тоді центру удару не існує. Це означає, що в цьому випадку опорні імпульси завжди є, тобто удар завжди передається на опори.
ДОДАТОК 1
Таблиця 1 – Зведення сил інерції точок тіла до головного вектора та
головного моменту
| № п/п | Вид руху | Головний вектор, головний момент |
| Поступальний |

| |
| Обертальний навколо осі z, перпендикулярної до площини симетрії |
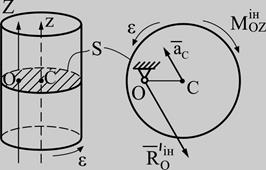 Вісь Оz Вісь Оz 

| |
Вісь Сz 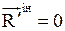

| ||
| Плоский в площині ху, паралельно площині симетрії | 

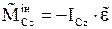
| |
| Інші рухи. т.О – центр зведення | 
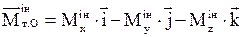
|
ДОДАТОК 2
Алгоритм визначення реакцій в’язей в “Динаміці” для
практичних моделей за допомогою принципу Д’Аламбера
 |
Дата добавления: 2015-10-29; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обертається навколо нерухомої осі | | | Professional Experience |