Постановка задачі, методика її розв’язування

ТЕОРЕТИЧНА МЕХАНІКА.

ДИНАМІКА

Конспект лекцій для студентів напрямку

“Інженерна механіка”

Деякі спеціальні питання динаміки.

Тема: Визначення динамічних реакцій опор

При обертанні тіла навколо нерухомої осі

Маріуполь, 2012

Карпенко Т.М. Теоретична механіка. Динаміка. Конспект лекцій для студентів напрямку “Інженерна механіка”. Деякі спеціальні питання динаміки. Тема: Визначення динамічних реакцій опор при обертанні тіла навколо нерухомої осі. – 2012

Затверждено на заседанні кафедры теоретичної і прикладної механики (протокол № 2 от 12.10.2012 р.).

Ухвалено методичною комисією механіко-машинобудівного факультету (протокол № 6 від 05.11.2012 р.).

Тема: ВИЗНАЧЕННЯ ДИНАМІЧНИХ РЕАКЦІЙ ОПОР

ПРИ ОБЕРТАННІ ТІЛА НАВКОЛО НЕРУХОМОЇ ОСІ

ЛІТЕРАТУРА

1. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. – М.: Высш.шк., 1983. – 575 с., ил. Глава 5 § 3, § 7.

2. Яблонский А. Курс теоретической механики. – М.: Высш. шк., 1984. – Т. 2. – 423 с. - § 102 – 104, § 110.

3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. - М.: ГИТТЛ, 1954. – Т.2. – 595 с. - §145, 146.

План

1. Постановка задачі, методика її розв’язування.

2. Зведення сил інерції точок тіла до головного вектора та головного моменту.

3. Рівняння для визначення повних реакцій опор, для визначення дина­мічних реакцій опор.

4. Умови відсутності динамічних реакцій.

5. Визначення імпульсів реакцій опор при ударі, умови їх відсутності.

Постановка задачі, методика її розв’язування

Маємо тіло відомої форми, масою m, тобто відомі його інерційні характеристики (згадаємо, що належить до них: маса, положення центру мас, моменти інерції: осьові, відцентрові, полярні).

Вважаємо, що нерухома вісь обертання не проходить через центр мас. Чому треба розглянути такий випадок? На практиці дуже складно досягти співпадання центру мас з віссю обертання, через те що:

­– в машинах матеріал, з якого виготовлені деталі, що обертаються – неоднорідний, тіло має мікроскопічні пустоти, зтираються деталі в місцях контакту і інше.

Як приклад, пропоную розглянути диск турбіни Лаваля, маса його m = 5 кг, обертається рівномірно з кутовою швидкістю n = 25000 об/хв. Центр мас (точка С) знаходиться від осі обертання на відстані ОС = 0,25 мм. (цю відстань називають ексцентриситетом, позначають е). Зверніть увагу е – дуже малий! Вважаємо, що цей диск знаходиться посередині між опорами А і В (рисунок 1).

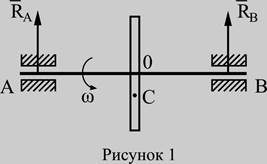Якщо диск не обертається, реакції опор (назвемо їх статичними) дорівнюють 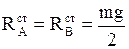. При обертанні реакції опор в 172 рази більші статичних реакцій! От чому розглядаємо наявність ексцентриситету.

Покажемо об’єкт вивчення (рисунок 2,а,б). На тіло діють відомі активні сили . На тіло накладені в’язі

- в точці А – підп’ятник,

- в точці В – підшипник.

Відстань між ними дорівнює l. Ми вже навчились з динамічного рівняння руху тіла визначати кутове пришвидшення ε і при відомій початковій швидкості кутову швидкість в довільний момент часу.

Як виглядає динамічне рівняння обертального руху з якого визначається ε? .

Позначимо осі координат Ахуz. Наша мета: визначити реакції опор . Скільки маємо невідомих? X_A, Y_A, Z_A, X_B, Y_B – п’ять невідомих. Задачу будемо розв’язувати методом кінетостатики (принципом умовного зрівноваження сил Д’Аламбера).

Згадаємо рівняння рівноваги за принципом Д’Аламбера: сума головних векторів активних сил, реакцій в’язей і Д’Аламберових сил інерції дорівнює нулеві

сума головних моментів сил активних, реакцій в’язей і Д’Аламберових сил інерції відносно довільної точки (візьмемо точку А) дорівнює нулеві.

Як ми діяли в розділі “Статика” при визначенні реакцій в’язей? Був такий алгоритм:

1. Об’єкт вивчення.

2. Схема сил, що діють на вільний об’єкт.

3. Вид системи сил.

4. Рівняння рівноваги, та їх розв’язок.

Будемо дотримуватись такої ж послідовності дій. Тільки тепер на схемі сил, крім активних і реакцій в’язей, повинні бути головний вектор та головний момент Д’Аламебрових сил інерції.

Як звести сили інерції точок тіла до головного вектора та головного момента в випадках, коли тіло має площину матеріальної симетрії, ми вже розглядали (таблиця 1 в Додатку). Якщо тіло довільної форми результатів загальних нема. Тому § 2.

Дата добавления: 2015-10-29