Missing operator, comma or semicolon

Рис. 2. Правильная запись вычисления функции на одномерном (а) и многомерном (б) массивах и неправильная (в) (пропуск точки с запятой после первого оператора)

12. Если не указана переменная для значения результата вычислений, то MATHLAB назначает такую переменную с именем ans.

13. Результат вычислений выводится в строках вывода (без знака»).

14. Для вычисления функции на одномерном или многомерном матричных массивах значений аргумента необходимо выполнить действия согласно рис.1.6.

В векторе (одномерном массиве) значения заключены в квадратные скобки и отделяются друг от друга пробелом (рис.3, а); в матрице (многомерном массиве) значения заключены тоже в квадратные скобки, причем, строки отделяются точкой с запятой (порядок следования строк: левая выше правой), а значения в каждой строке отделяются аналогично вектору (рис.3, б).

15. Если значения аргумента вычисляемой функции являются членами отрезка арифметической прогрессии с заданной разностью (шагом), то для записи аргумента применяется оператор «двоеточие:» – см. рис. 3. При разности, равной единице, ее запись в операторе можно опускать (см. рис. 3, б).

а) » x=1:2.5:16.5;Y=sin(x)

Y =

0.8415 –0.3508 –0.2794 0.7985 –1.0000 0.8038 –0.2879

б) » x=1:10;Y=sin(x)

Y =

Columns 1 through 7

0.8415 0.9093 0.1411 –0.7568 –0.9589 –0.2794 0.6570

Columns 8 through 10

0.9894 0.4121 –0.5440

в) x=[1:2.5:11.5; 2:6];Y=sin(x)

Y =

1327/1577 –851/2426 –1109/3969 1161/1454 –102108/102109

401/441 441/3125 –445/588 –677/706 –1109/3969

Рис. 3. Правильная запись вычисления функции на одномерном массиве аргумента в виде отрезка арифметической прогрессии (с разностями 2,5 (а) и 1 (б)) и в виде 2-строчной матрицы с теми же разностями (в)

14. Для правильной записи значений матрицы аргумента, когда ее строки являются отрезками арифметических прогрессий, необходимо руководствоваться правилами 14 и 15 одновременно.

15. Комментарии записываются в отдельную строку, помечаемую знаком процента (%)в первом знакоместе строки (см. рис. 4, а).

16. Разбиение строки с длинным выражением или комментарием на две производится установкой курсора перед переносимой на создаваемую вторую строку частью выражения и нажатием клавиш Shift + Enter (см. рис. 4, б) – двукратное разбиение выражения х = [23 45 67 45] на три строки).

17. Соединение двух строк в одну в программе или в выражении производится установкой курсора в начало второй строки и нажатием клавиш Shift + Backspace (рис. 4, в) – соединение двух строк с выражениями 67 и 45]).

а) »x=[0.5 0.7 1];Y=sin(x)

% Комментарии размещаются в отдельных строках

Y =

0.4794 0.6442 0.8415

б) » x=[23 45 67 45]

x =

67 45

в) » x=[23

67 45]

x =

45 67 45

Рис. 4. Ввод комментария в вычисляемое выражение или программу (а), разбиение

первой строки на три (б), объединение 3-й и 2-й строк (в)

18. Вычисляемое выражение сразу после завершения вычисления можно ввести вновь в текущее место ввода нажатием кнопки «стрелка вверх» ↑ (для изменения величин аргументов или коррекции выражения).

Повторное нажатие кнопки ↑ заменит текущие условия на условия, им предшествующие: этот процесс можно повторять многократно, добиваясь вызова в место ввода все более ранних вычислительных условий.

Ранее вычислявшееся выражения можно быстро вставить в место ввода путем выделения его левой кнопкой мышки (кнопка далее отпускается) и небольшого протягивания его вниз повторно нажатой левой кнопкой: MATHLAB сам вставит выделенное выражение.

19. Ранее примененную функцию можно вставить в командное окно через копирование её из окна Command History (Протокола команд), в котором все ранее использованные команды и функции сохраняются до тех пор, пока пользователь не удалит их.

20. Чтобы сохранить данные вычислений в окне управления (выражения, программы, результаты или их части) для повторного вызова и работы, необходимо:

• выделить данные,

• скопировать их в буфер,

• вызвать редактор-отладчик m -файлов через меню «Файл-Создать-m-файл», либо командой edit в командном окне,

• вставить скопированные данные в открывшийся новый m -файл и сохранить его через меню редактора File-Save As… («Файл-Сохранить как»).

21. Для продолжения вычислительной работы в окне управления с данными, сохраненными по правилам п.20, необходимо через меню «Файл-Открыть» открыть требуемый файл, выделить в нем требуемые для работы фрагменты, скопировать их в буфер и вставить в текущее место ввода окна управления.

Рассмотрим применение перечисленных выше правил для выполнения вычислений.

Использование переменных. Результат вычислений можно присвоить любой переменной, определенной пользователем. Имя переменной должно начинаться с буквы и может состоять из букв, цифр и символа подчеркивания. Система MATHLAB различает строчные и прописные буквы в именах переменных (A и a – это разные переменные). Знак = соответствует операции присваивания. Значения переменных, вычисленные в течение текущего сеанса работы, сохраняются в специально зарезервированной области памяти компьютера, называемой рабочим пространством (Workspace). Использование переменных рассмотрено в примере 1.

Пример 1. Использование переменных

Комментарии к вычислениям:

Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.

Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.

Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.

Использование MATHLAB как калькулятора иллюстрирует также пример 2.

Пример 2. Использование MATHLAB как калькулятора

Комментарии к вычислениям:

Нажатие клавиши Enter.

Результат присваивается переменной с именем ans

Результат выводится в формате с плавающей точкой. Такая запись означает 1.5031·10³.

Длинные выражения можно записать в нескольких строках с использованием в качестве знака переноса символа многоточия ….

Использование массивов. В системе MATHLAB также используются массивы, математической формой представления которых являются матрицы. Напомним основные действия над матрицами и их реализацию в MATHLAB.

1. Присвоение значений матрице. Простейшей операций с матрицей является ее создание. Для создания столбца необходимо указать его имя, знак равенства и в квадратных скобках через запятую или через пробел перечислить значения элементов. Например: А=[1 2 3 4 5]. В случае если необходимо создать столбец чисел, то в качестве разделителя выступает символ точка с запятой, например: B=[1;3;5;7]. Для создания квадратной или прямоугольной матрицы необходимо чередовать оба этих способа, например:

С=[ 1 2 3; 4 5 6; 7 8 9 ].

2. Создание матриц специального вида. В математике встречаются матрицы специального вида, часто используемые при решении прикладных задач. Ниже приведен ряд из них:

Единичная матрица, рис. 5, а. В единичной матрице все элементы равны нулю, кроме элементов стоящих на главной диагонали и равных единице. Для создания единичной матрицы необходимо подать команду

<Имя матрицы>=eye(<Размер>).

Например: A=eye(4,4).

Единичная матрица может быть только квадратной.

Матрица со всеми единицами, рис. 5, б. Эта матрица содержит единицы во всех ячейках. Для создания матрицы необходимо указать

<Имя матрицы>=ones(<Кол-во строк>, <Кол-во столбцов>).

Например: A=ones(3, 4).

Нулевая матрица, рис. 5, в. Эта матрица содержит во всех своих ячейках одни нули. Для создания необходимо выполнить следующую команду:

<Имя матрицы>=zeros(<Кол-во строк>, <Кол-во столбцов>).

Например: A=zeros(4, 2).

Случайная матрица, рис. 5, г. Все значения этой матрицы получаются с генератора случайных чисел. Для создания такой матрицы необходимо задать следующую команду:

<Имя матрицы>=rand(<Кол-во строк>, <Кол-во столбцов>).

Например: A=rand(6, 3). По умолчанию в качестве элементов матрицы используются вещественные числа.

а б в г

Рис.5. Специальные матрицы

Доступ к ячейкам матрицы. Для доступа к ячейкам матрицы необходимо указать имя матрицы, номер строки и номер столбца. Нумерация строк и столбцов ведется с единицы. Номера пишутся в круглых скобках. Общий формат записи

<Имя массива>(<Номер строки>, <Номер столбца>).

Например: A(1,2).

Умножение матрицы на скаляр. В математике для всех матриц определена операция умножения матрицы на скаляр (число). Все значения матрицы в этом случае умножаются на это число:

Сложение, вычитание скаляра из матрицы. Кроме операции умножения матрицы на скаляр для матрицы и скаляра определены операции сложение и вычитания. Действия так же выполняются с каждой ячейкой матрицы отдельно:

Сложение (вычитание) матриц. Эта операция допустима только с матрицами одинакового размера. При выполнении операции действие выполняется с соответствующими друг другу ячейками:

Произведение матриц. При выполнении операции перемножения матриц выполняется последовательное умножение строки на вектор. При этом количество столбцов в первой матрице должно равняться количеству строк во второй матрице. Матрица результата будет иметь количество столько же строк, сколько и в первой матрице, и количество столбцов равное количеству столбцов во второй матрице:

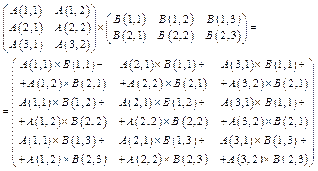
Присвоение матрице математического выражения. Организация всех переменных системы MATHLAB как матрицы вызывает следующие ограничения применения их в выражениях.

Пример 3.

t=1:5

t= 1 2 3 4 5

y=cos(t)

y=1 0.5 –0.4 –1 –0.6 0.2

z=y/t

z=–0.08

Результат – получается единственное число, а ожидали функцию z(t)=cos(t)/ t!

Для организации поэлементного выполнения арифметических операций предусмотрена специальная форма их записи: «.op». Для приведенного выше примера применение операций деления одного массива на другой в виде «./» дает следующий результат:

z=y./ t

z= 0.5403 –0.2081 –0.3300 –0.1634 0.0567.

Использование массивов рассмотрено в примере 4.

Пример 4. Использование массивов.

Комментарии к вычислениям:

Элементы массива задаются в квадратных скобках.

Другой способ задать массив в виде x:y:z, где x – первый элемент массива, z – последний элемент массива, y – приращение каждого следующего элемента над предыдущим. Здесь элементами массива будут 2 2,5 3 3,5 4.

Сложение и вычитание массивов осуществляется поэлементно.

Операции поэлементного умножения и деления массивов обозначаются: .* и. /

Взятие функции от каждого элемента массива. В результате получится массив той же размерности.

Использование отдельных элементов массива. Номер элемента указывается после имени переменной массива в круглых скобках. Нумерация элементов начинается с единицы.

Сложение и умножение всех элементов массива на число.

Для генерации векторов пользователю предоставляется следующая команда:

<Имя вектора>=<Начальное значение>:<Шаг>:<Конечное значение>.

Например: Х=6:0.2:26.

Ответ: X=

6.0000 6.2000 6.4000 6.6000 6.8000 7.000

Программирование в ППП MATHLAB. Приемы разработки программ в MATHLAB в своей основной форме совпадают с аналогичными программами, разрабатываемыми в большинстве языков программирования.

Цикл for… end. Для данного n,оператор

x =[];for i =1:n x=[x,i.2 ],end

или

x =[];for i =1:n x =[x,i.2 ],end

создает определенный вектор размерности n,а оператор

x =[];for i =n:-1:1,x=[x,i.2 ],end

создает вектор с теми же элементами, но размещенными в обратном порядке.

Заметим, что матрица может быть пустой (например, в случае оператора x=[].)

Последовательность операторов

for i =1:m

for j =1:n

H(i,j)=1/(i+j-1);

End

End

H

создаст и напечатает на экране матрицу Гильберта размерности m×n. Точка с

запятой, которая завершает внутренний оператор, предотвращает вывод на экран ненужных промежуточных результатов, в то время как последний оператор H выводит на экран окончательный результат.

Цикл while… end. В общем виде цикл while записывается в виде

while <условие>

<операторы>

End

<Операторы> будут повторяться до тех пор, пока <условие> будет оставаться истинным. Например, для заданного числа a приведенная далее последовательность операторов вычислит и выведет на дисплей наименьшее неотрицательное число n,такое что 2n < a:

n=0;

while 2 ^n <a

n=n +1;

End

n

Условный оператор if… end. В общем виде простой оператор if используется следующим образом:

if <условие>

<операторы>

End

<Операторы> будут выполняться только если <условие> истинно. Возможно также множественное ветвление, что демонстрируется приведенным далее примером.

if n <0

parity =0;

elseif rem(n,2)==0

parity =2;

Else

parity =1;

End

При использовании двухвариантного условного оператора часть, связанная с elseif, конечно, не используется.

Оператор переключения case… end. При необходимости построить конструкцию ветвления с более чем двумя логическими условиями удобнее использовать не вложенные операторы if,а оператор переключения switch...case. Этот оператор имеет следующую структуру:

switch <выражение>

%<выражение>-это обязательно скаляр или строка

case <значение1>

Операторы

%выполняется, если <выражение>=<значение1>

case <значение2>

Операторы

%выполняется, если <выражение>=<значение2>

...

Otherwise

Операторы

%выполняется, если <выражение>не совпало

%ни с одним значением

End

Условия (операторы отношения). В MATLAB используются следующие операторы отношения:

Обозначение	Значение
<	меньше чем
>	больше чем
<=	меньше или равно
>=	больше или равно
==	равно
~=	не равно

Отметим, что знак = используется в операторах присваивания, в то время как

знак == используется в операторах отношения. Операторы отношения (или, другими словами, логические переменные, которые они создают) могут объединяться с помощью логических операторов:

Обозначение	Значение
&	И
|	ИЛИ
~	НЕ

Когда эти операторы применяются к скалярам, то результатом является тоже

скаляр 1 или 0 в зависимости от того, является ли результат истиной или ложью. Попробуйте вычислить 3 <5, 3>5, 3==5 и 3==3. Когда операторы отношения применяются к матрицам одного размера, результатом является матрица того же размера, у которой в качестве элементов стоят 0 или 1, в зависимости от соотношения между соответствующими элементами исходных матриц. Попробуйте вычислить a=rand(5), b=triu(a), a ==b. Операторы while и if интерпретируют отношение между матрицами как истинное в том случае, если результирующая матрица не имеет нулевых элементов.

Так, если вы хотите выполнить оператор в том случае, когда матрицы A и B

полностью совпадают, вы можете написать

if A ==B <операторы>end

но если вы хотите выполнить оператор в том случае, когда матрицы A и B не равны, вы должны ввести

if any(any(A.=B))<оператор>end

или, что проще,

if A ==B else <оператор>end.

Заметим, что конструкция

if A.=B, <оператор>, end

почти наверняка не даст того, что нужно, поскольку оператор будет выполняться, только если каждый элемент матрицы A будет отличаться от соответствующего элемента матрицы B. Для сведения матричных отношений к вектору или скаляру можно воспользоваться функциями any и all. В предыдущем примере необходимо использование функции any два раза, поскольку эта функция – векторная.

Функция find. Оператор k=find(x) возвращает вектор k номеров ненулевых элементов вектора/матрицы x. Если x – матрица, то при определении индексов она рассматривается как вектор, образованный последовательно соединенными столбцами матрицы. Вектор find(x) можно использовать совместно с операторами отношения, поскольку результатом применения оператора отношения к матрицам является матрица из 0 и 1 (ложь или истина). Таким образом, можно с помощью одного оператора find определить и записать сразу все индексы матрицы, удовлетворяющие некоторому условию. Если при этом вспомнить, что оператор цикла for допускает форму for k=KK,где KK – целый вектор, то удобно использовать их вместе. Например, если вам необходимо выполнить <оператор> только для тех элементов матрицы, которые больше 3,то удобно это сделать следующим образом:

for i=find(A>3)

<оператор>

End;

При отладке выражений и программ в окне Редактора-отладчика сообщения об ошибках выдаются в командное окно MATLAB.

М-файлы бывают двух типов: сценарии и функции. Для их создания необходимо вызвать редактор m -файлов командой edit в командном окне либо последовательностью File→New→M-file из меню командного окна

M -файл-сценарий, именуемый также Script -файлом, является просто записью серии команд без входных и выходных параметров. Он имеет следующую структуру:

%Основной комментарий

%Дополнительный комментарий

Дата добавления: 2015-10-28