Риск-модели атак на компьютерные системы

Существует на практике задача анализа многократно повторяющихся сетевых атак на компьютерные системы, где успешность операции характеризует количество проникновений в систему k при проведении n атак [48]. Считая вероятность такого проникновения для единичной атаки, равной p₀, а величину ущерба каждого проникновения u₀ (без учета всех последствий, которые также являются предметом дальнейшего противоборства), закон дискретного распределения вероятности наступления ущерба в общем виде можно записать

P = P (n, k, p₀) и U = ku₀.

Качественно эту запись иллюстрирует рис. 3.43, а [49]. Дальнейшее нормирование по максимально допустимому ущербу u_max = nu₀, переводит описание процесса в единичное пространство (рис. 3.43, б), а

P = P(k/n, p₀) и .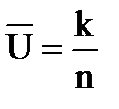

Отсюда имеем выражение для риска

R_isk(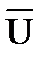) = 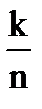P(k/n,p₀)

и соответствующий ему график рис. 3.43, в.

Интегральный риск (вероятность наступления ущерба, не превышающего заданной величины u_i) соответственно будет равен

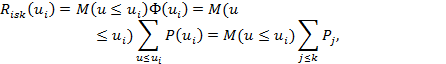
где 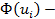интегральная функция распределения ущерба.

Дополнение 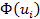до единицы дает вероятность того, что ущерб превышает

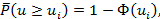
откуда соответствующий интегральный риск превышения

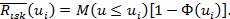
Отсюда защищенность системы по уровню ущерба будет равна

По аналогии вероятность попадания ущерба в интервал (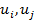 ] определяется как

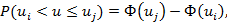
а усредненный риск соответственно будет равен

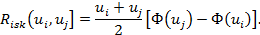
Риск непопадания в данный интервал соответственно определяется выражением

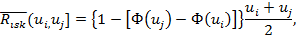
а защищенность системы от ущербов интервала 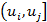будет равна

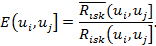
Математическое ожидание (среднее значение) ущерба для дискретного распределения вероятностей суммой элементарных рисков

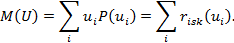
Дисперсия ущерба для дискретного распределения определяется через риск следующим образом

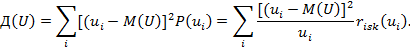
По аналогии через элементарный риск могут быть найдены мода, медиана, ассиметрия и прочие параметры ущерба [50].

Защищенность системы (эффективность защиты) для подобных дискретных распределений можно оценить следующим образом

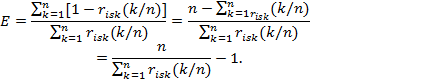
Интервалы дискретизации в единичном интервале здесь будут одинаковыми как для числителя, так и для знаменателя. И потому могут не учитываться [51].

К примеру, для биномиального распределения по формуле Бернулли вероятность равна

.

На основании вышеизложенного

.

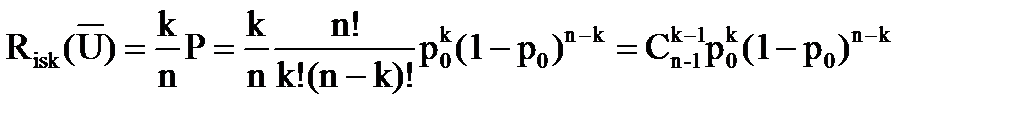Целая группа дискретных распределений рассматривает испытания до первого «успеха», т.е. анализирует вероятное количество атак на систему до первого ее вскрытия (рис. 3.44, а). В этом случае ущерб при всех k будет одинаков u₀, и, следовательно, кривая огибающей риска (в зависимости от номера атаки, а не от ущерба) будет иметь аналогичный вид (рис. 3.44, б) [52].

Причем, в отличие от биномиального распределения, ограничений на k здесь не существует, и оценку защищенности мы сможем провести только для каждого текущего k в отдельности.

U

∙ ∙ ∙

∙ ∙ ∙

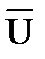
P()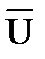

∙ ∙ ∙

∙ ∙ ∙

P(U)

nu₀

∙ ∙ ∙

u₀

∙ ∙ ∙

ku₀

а) б)

∙ ∙ ∙

∙ ∙ ∙

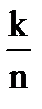
R_isk()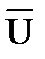

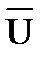
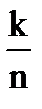
в)

Рис. 3.43. Дискретное распределение вероятности (а, б) и риска (в) в зависимости от ущерба проникновения в систему в результате многократных кибернетических атак

Думается, что это вполне корректно, ибо после «успеха» данный эксперимент завершается, поэтому

.

∙ ∙ ∙

∙ ∙ ∙

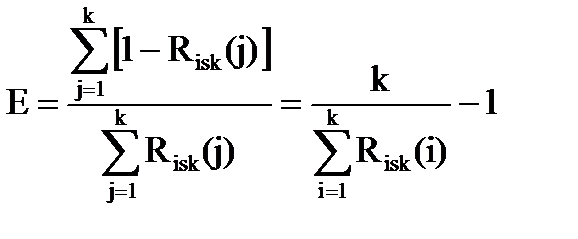1 2

a)

k

k

P(k)

∙ ∙ ∙

∙ ∙ ∙

R_isk(k)=P(k)u₀

1 2

k

k

б)

Рис. 3.44. Дискретное распределение вероятностей (а) и риска (б) в зависимости от номера испытаний

Отсюда для геометрического распределения риска атак (рис. 3.45) имеем

R_isk(k) = p₀ (1-p₀)^k

и защищенность системы равна

.

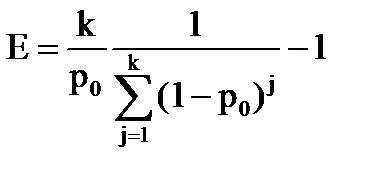По аналогии для распределения Паскаля

R_isk(k) = m C_k^m+k-1 p₀^m(1-p₀)^k

имеем

.

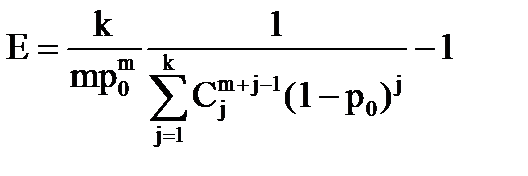R_isk(k)

1 2

k

p₀

В этом случае оценивается вероятность m-кратного проникновения в систему (mu₀) в результате (m+k) атак [53].

Рис. 3.45. Дискретное распределение риска для геометрического распределения

Каждая из дискретных моделей атак имеет вполне определенную область применения:

- биномиальное – вероятность появления k успешных атак в n независимых атаках, когда вероятность p₀ проникновения в систему в каждом испытании постоянна (извлечения с возвращением);

- геометрическое – вероятность того, что потребуется k атак Бернулли, прежде чем будет осуществлено проникновение в систему;

- Паскаля – вероятность того, что потребуется провести k атак Бернулли для появления s успешных проникновений в систему;

- Пуассона – вероятность успеха k независимых атак в данном интервале времени t, когда события происходят с постоянной интенсивностью l;

- мультиномиальное – вероятность успеха i-й атаки k_i раз в n испытаниях, когда вероятности событий p₀ постоянны и события k_i образуют полную группу;

- гипергеометрическое – вероятность нейтрализации k атак в выборке объема m атак, взятой из совокупности объема n, которая содержит k проникновений в систему (извлечения без возвращения) [54].

С учетом вышеизложенного рекомендуется осуществлять оценку рисков и защищенности распределенных компьютерных систем, атакуемых извне.

Для риск-анализа распределений обязательно нужно найти вероятность успеха k-ой атаки, которая аналитически представляет собой следующую сумму произведений

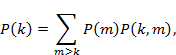
где 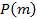– вероятность того, что m из n атак на систему придутся на компоненты распределенной системы;

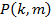– вероятность того, что k из m атак уязвимости системы достигнут успеха и будет нанесен ущерб.

Тогда интегрально риск может быть измерен в виде матожидания ущерба u

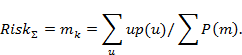
Используем данную концепцию для аналитического риск-анализа.

Пусть распределенная компьютерная система состоит из N компонентов, M из которых уязвимы для рассматриваемого типа атак. За анализируемый период времени рассматриваемая система подвергается данным атакам в количестве n. Тогда вероятность того, что m из n атак придутся на уязвимые компоненты системы по гипергеометрическому закону [56] составит

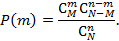
Далее, полагая что вероятность реализации уязвимости (успеха атаки) для каждого уязвимого компонента системы усреднено равна p, имеем биноминальное распределение

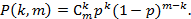
В случае совмещения вышеуказанных событий, получаем вероятность успеха k атак на компоненты системы в следующем виде

Отсюда, при условии усредненного значения ущерба от единичной атаки 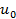, представляется определить риск возникновения k успешных атак

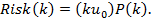
Соответственно интегральный риск (матожидание ущерба) в данном случае составит

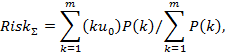
где, ввиду рассмотрения полной группы событий, допустим инвариант

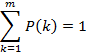
Практическую сложность для численных расчетов 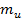представляет сомножитель 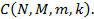Однако, возможно аналитическое упрощение

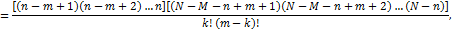
которые существенно экономит вычислительные затраты.

Предложенная модель открывает перспективу обобщенного риск-анализа атакуемых и частично уязвимых компонентов системы.

Дата добавления: 2015-10-26