Расчет рисков распределенных систем на основе параметров рисков их компонентов

При создании защищенных автоматизированных систем, рассмотрение ущерба как случайной величины довольно распространено. Причем описание принято осуществлять с использованием различных законов распределения, среди которых наибольшее популярностью пользуются регулярные законы. В данном классе существенное практическое применение нашло экспоненциальное (x>0) семейство: экспоненциальный и логнормальный законы; гамма-распределение; распределение Эрланга, Вейбула и Релея.

Рассмотрим это семейство в контексте построения риск-моделей атакуемых систем, имея ввиду следующие обозначения:

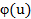– плотность вероятности наступления ущерба u;

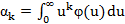– k-ый начальный момент ;

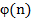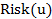=u 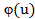– риск наступления ущерба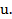

Будем исходить из того, что на основе статистики определен закон распределения 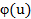, т.е. выдвинута и доказана гипотеза (скажем, с помощью критериев Пирсона или Колмогорова), определены параметры 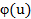, соответствующие статданным. Когда оценка рисков компонентов распределенной системы осуществлена, т.е. известны законы распределения риска и найдены его параметры для каждого компонента, представляется возможность рассчитать риск системы в целом. При этом, будем исходить из того, что ущербы, возникающие в ее компонентах при отказах и атаках на них слабо коррелированны между собой. Тогда ожидаемый общий ущерб системы можно найти как сумму ущербов в отдельных ее компонентах. Причем это допустимо не только для детерминированных, но и для случайных величин. С другой стороны относительная независимость этих параметров открывает перспективу соответствующих вероятностных оценок, рассматривая вероятность наступления общего ущерба как произведение вероятностей возникновения ущербов в компонентах системы. В этой связи может быть предложено следующее выражение оценки риска

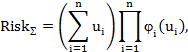
где: 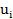– мера ущерба в i-ой компоненте;

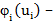плотность вероятности наступления ущерба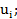

n – количество компонентов системы.

В случае использования экспоненциального семейства распределений последнее выражение примет вид

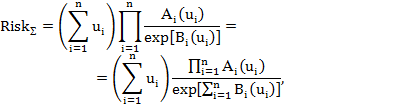
где 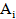и 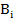– функции ущерба i-ого компонента, определенные на основе соответствующего типа регулярного распределения экспоненциального семейства.

Данное выражение может быть конкретизировано, если законы распределения для ущербов в компонентах однотипны (имеют общие выражения) и отличаются друг от друга лишь параметрически. Такое в принципе возможно при однотипности компонентов, различающихся только настройкой на свою задачу. В этом случае, к примеру, для экспоненциального распределения имеем выражение для общего риска системы

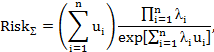
где 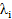– параметр распределения плотности вероятности наступления ущерба в i-ой компоненте.

По аналогии можно записать выражение общего риска системы при различных распределениях:

– для распределения Релея

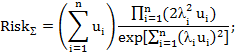
– для гамма-распределения

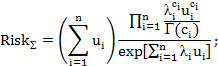
– для распределения Эрланга

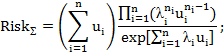
для распределения Вейбулла

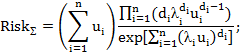
– для логнормального распределения

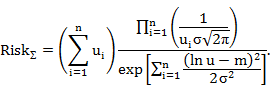
Для полученных выражений остается открытым вопрос о том, какие значения 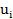следует принимать во внимание. Здесь возможны по крайней мере два варианта: пиковая и средняя оценка.

При пиковой оценке используются координаты максимума риска (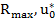) и общее выражение будет выглядеть следующим образом

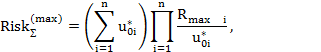
где 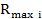– значение максимума риска в i-ой компоненте системы;

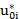– значение ущерба, при котором имеет место быть пик риска в i–ой компоненте системы, т.е. мода риска.

Для различных типов экспоненциального семейства регулярных распределений последнее выражение можно переписать в следующем виде:

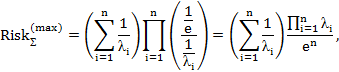
при ,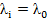

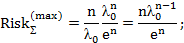
– для распределения Релея

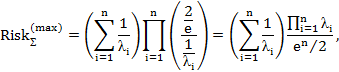
при ,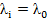

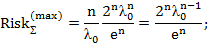
– для Гамма распределения

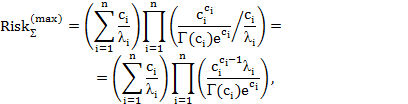
при ,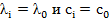

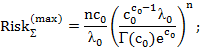
– для распределения Эрланга

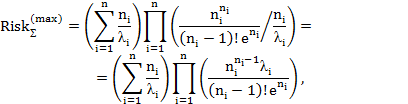
при ,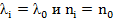

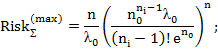
для распределения Вейбулла

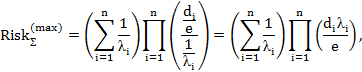
при ,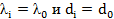

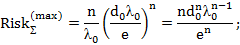
– для логнормального распределения

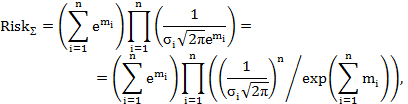
при ,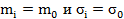

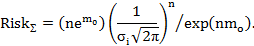
Для удобства полученные выражения сведены в табл. 2.12.

Таблица 2.12

Аналитические выражения для расчета общего риска при пиковых оценках риска в компонентах

Вид используемого закона распределения	Аналитическое выражение для расчета общего риска при пиковых оценках риска в компонентах
Экспоненциальный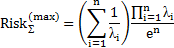
Релея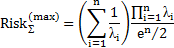
Гамма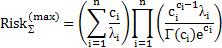
Эрланга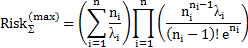
Вейбулла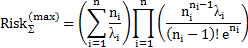
Логнормальный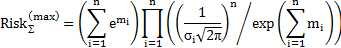

Алгоритм расчета общего риска в данном случае должен предусматривать прежде всего ввод данных о виде и параметрах распределений плотности вероятности наступления ущерба в каждой из компонент распределенной системы. Далее необходимо определить (в зависимости от вида распределения) координаты пика для всех компонентов системы. Полученные данные в результате следует использовать для расчета общего риска. Блок-схема данного алгоритма представлена на рис. 2.5.

При использовании усредненных оценок в компонентах общий риск системы можно рассчитать с помощью выражения

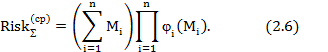
В случае однотипных распределений плотности вероятности наступления ущерба в компонентах последнее выражение может быть конкретизировано:

– для экспоненциального распределения

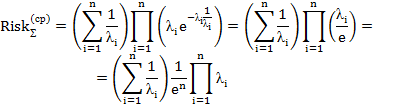
при ,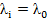

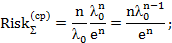
– для распределения Релея

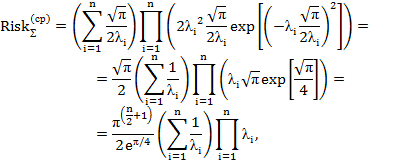
при ,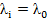

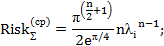
– для гамма-распределения

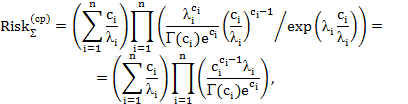
при ,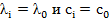

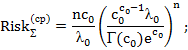
– для распределения Эрланга

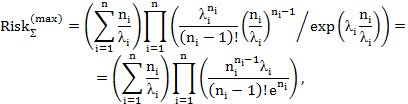
при ,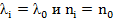

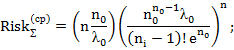
для распределения Вейбулла

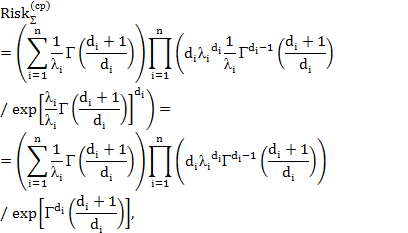
при ,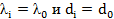

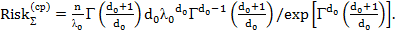
– для логнормального распределения

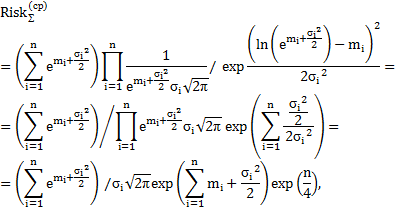
при ,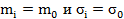

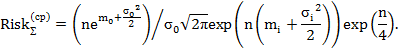
Начало

Конец

Расчет координат пикового ущерба i- ой компоненты системы

Расчет общего риска системы с помощью выражения (2.2)

i=n

i=i+1

Полученные выражения для удобства сведены в табл. 2.13.

Рис. 2.5. Блок-схема алгоритма расчета общего риска системы на основе пиковых оценок риска в ее компонентах  

Ввод данных о виде и параметрах распределения плотности вероятности наступления ущерба для i -го компонента системы

Таблица 5.13.

Аналитические выражения для расчета общего риска при усредненных оценках риска в компонентах

Вид используемого закона распределения	Аналитическое выражение для расчета общего риска при усредненных оценках риска в компонентах
Экспоненциальный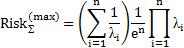
Релея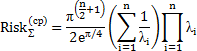
Гамма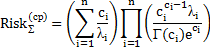
Эрланга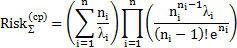
Вейбулла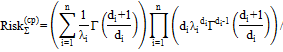
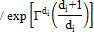
Нормальный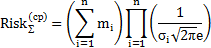
Логнормальный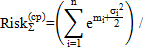

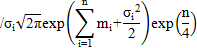
Алгоритм расчета общего риска системы при усредненных оценках риска в ее компонентах прежде всего включает ввод данных о виде параметрах распределения плотности вероятности наступления ущерба в компоненте. Далее находятся координаты среднего значения для ущерба в данной компоненте. Цикл с перебором по всем имеющимся в системе компонентам завершается расчетом по выражению (2.6). Блок-схема данного алгоритма изображена на рис. 2.6.

Предложенные таблицы 2.12 и 2.13 могут упростить расчет общего риска распределенной системы с помощью алгоритмов (рис. 2.5 и 2.6).

Начало

Ввод данных о виде и параметрах распределения плотности вероятности наступления ущерба для i -го компонента системы

Расчет координат усредненного ущерба i- ой компоненты системы

i=i+1

Рис. 2.6. Блок-схема алгоритма расчета общего риска системы на основе усредненных оценок риска в ее компонентах

Рис. 2.6. Блок-схема алгоритма расчета общего риска системы на основе усредненных оценок риска в ее компонентах (продолжение)  

Конец

Расчет общего риска системы с помощью выражения (2.6)

i=n

Дата добавления: 2015-10-26