Алгоритмическое обеспечение риск-анализа систем в диапазоне ущербов

Рассмотрим экспоненциальное семейство распределений плотности вероятности 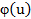наступления ущерба с областью определения u>0. К таковым относятся логнормальное, экспоненциальное и гамма-распределения, распределения Релея, Вейбула и Эрланга. Соответствующие им аналитические выражения риска представлены в табл. 2.11.

Анализ аналитических выражений риска (табл. 2.11) позволяет для первых пяти видов распределения сделать следующее обобщение

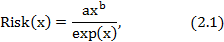
где: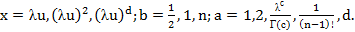

Таблица 2.11

Анализ аналитических выражений риска

Вид распределения плотности вероятности ущерба	Аналитическое выражение для риска
Экспоненциальный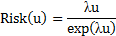
Релея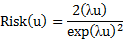
Гамма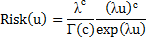
Эрланга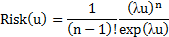
Вейбулла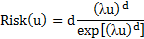
Логнормальный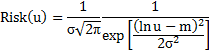

С целью нахождения значений ущерба по заданному уровню риска для (2.1) составим следующее уравнение

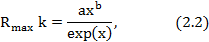
где: 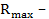пиковое значение риска;

k– коэффициент (k<1) задающий уровень отсчета от .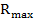

Для поиска решения уравнения (2.2) прологарифмируем его

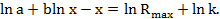
Далее разложим натуральный логарифм в ряд

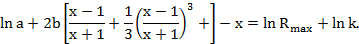
Ограничимся первыми двумя членами ряда. Здесь погрешность составит для x=2 менее 1%, а для x=4 около 3%. Принимая данную погрешность допустимой, запишем уравнение

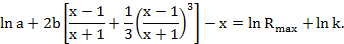
Произведем следующую замену переменных

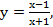где область определения -1<y<1.

Соответственно обратное преобразование будет иметь вид

В результате получим уравнение

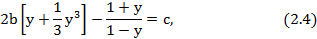
где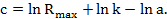

Приводя (2.4) к общему знаменателю, получаем

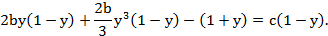
Далее сгруппируем члены по степеням и в результате получим уравнение четвертой степени

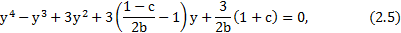
которое, как известно может быть решено в аналитическом виде. Два корня этого уравнения будут комплексными числами, а два других, имеющими физический смысл, действительными. Для них следует произвести обратное преобразование (2.3) и получить значения 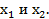Графически это решение можно проиллюстрировать с помощью рис. 2.11. Соответствующий алгоритм представлен на рис. 2.4.

R_max

Risk

x

x₂

x₀

x₁

R_max k

Начало

Рис. 2.3. Границы ущербов по заданному уровню риска

Конец

Расчет промежуточных параметров (2.4)

Решение уравнения (2.5)

Выполнение обратного преобразования

Ввод значений параметров распределения (2.1)

Рис. 2.4. Блок-схема алгоритма поиска граничных значений ущерба по заданному уровню риска

По аналогии для логнормального распределения плотности вероятности наступления ущерба посредством логарифмирования может быть получено уравнение

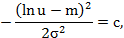
где: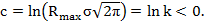

Осуществляя замену 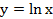и раскрывая скобки, имеем уравнение

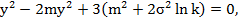
решением которого являются корни

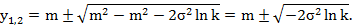
Отсюда

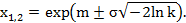
Расчет данного выражения не представляет труда.

Полученные результаты служат методической и алгоритмической основой для нахождения границ ущербов (диапазона ущерба) для заданного уровня риска, что является важной задачей риск-анализа.

Узкополосность характеристики риска (рис. 2.3) может быть оценена следующим образом

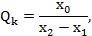
где 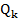– значение данного параметра по уровню 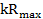. Для логнормального распределения она имеет следующий вид

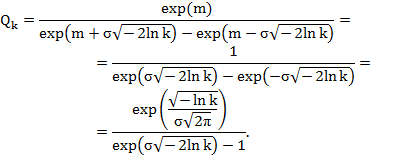
Как видно, узкополосность характеристики не зависит от n и определяется параметром . При отсчете по уровню 3дБ имеем .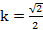

Дата добавления: 2015-10-26