Расчет параметров рисков для компонентов систем

Многоальтернативность и непредсказуемость атак на компоненты системы зачастую не оставляют надежд для детерминированного описания этих процессов и возникающих в результате их реализации ущербов. Поэтому при создании защищенных автоматизированных систем, рассмотрение ущерба как случайной величины представляется вполне обоснованным. В этом случае описание принято [2] осуществлять с использованием различных законов распределения, среди которых наибольшее популярностью пользуются регулярные законы. В этом классе наиболее практическое применение нашли законы, определенные на 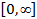: экспоненциальный и логнормальный законы; гамма-распределение; распределения Эрланга, Вейбула и Релея [3,4].

Рассмотрим это семейство в контексте построения риск-моделей атакуемых систем, имея ввиду следующие обозначения:

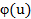– плотность вероятности наступления ущерба u;

– k-ый начальный момент ;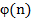

– среднее значение u;

– k-ый центральный момент ;

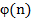– среднеквадратическое отклонение u от среднего значения M;

– мода, соответствующая максимальному значению ;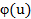

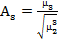– ассиметрия, характеризующая отклонение кривой 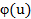от симметрии;

– эксцесс, характеризующий островершинность 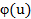в сравнении с нормальной кривой.

Опираясь на этот параметрический базис, постараемся проанализировать функцию риска, которая в общем случае имеет следующий вид

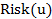=u .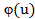

При этом, будем исходить из того, что на основе статистики определен закон распределения 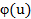, т.е. выдвинута и доказана гипотеза (скажем, с помощью критериев Пирсона или Колмогорова), определены параметры 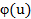, соответствующие статданным.

На основании вышеизложенного найдем аналитические выражения для параметров риска через перечисленные параметры плотности вероятности наступления ущерба. Рассмотрим прежде начальные моменты риска

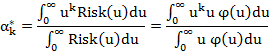
Отсюда среднее значение ущерба для кривой риска равно .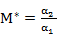

Соответственно для центральных моментов риска имеем,

Так, для второго центрального момента риска получаем выражение

Отсюда среднеквадратическое отклонение будет равно

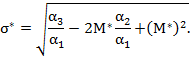
Следует заметить, что подобное отклонение может быть найдено относительно моды риска 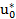, которая может быть определена из решения следующего уравнения

Для оценки ассиметрии и островершинности кривой риска необходимо найти подобные аналитические выражения для третьего и четвертого центральных моментов риска:

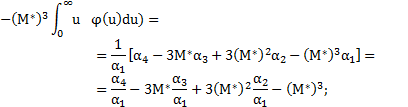
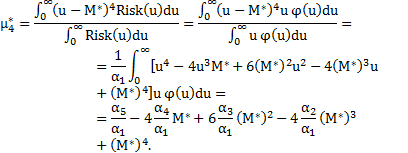
Осуществляя подстановку , имеем:

Далее аналитически можно выразить ассиметрию и эксцесс риска.

Для удобства дальнейшего анализа, вcе они сведены в нижеприведенную табл. 2.1.

Таблица 2.1

Обобщенные аналитические выражения для расчета параметров риска

Параметры риска	Аналитические выражения параметров
Начальные моменты
Среднее значение ущерба
Второй центральный момент
Среднеквадратическое отклонение ущерба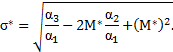
Третий центральный момент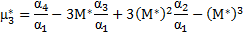
Четвертый центральный момент
Ассиметрия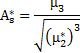
Эксцесс
где -начальные моменты плотности вероятности наступления ущерба.

Как видно, для проведения численных расчетов вышеуказанных параметров достаточно знать величины первых начальных моментов плотности вероятности наступления ущерба. Для рассматриваемого семейства это представляется возможным (табл. 2.2).

Что же касается моды, то для рассматриваемого семейства экспоненциальных распределений можно сделать следующее обобщение

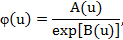
где функции и определяются видом распределения (табл. 2.2).

Поиск экстремума риска сводится к решению уравнения

или

Решение этого уравнения 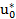позволит найти пик риска Представленные параметры достаточно полно характеризуют кривую риска.

Для иллюстрации рассмотрим показательное (экспоненциальное) распределение, где

Соответственно риск имеет вид

Отсюда для поиска моды имеем

или

Решением последнего уравнения является мода

Таблица 2.2

Основные параметры экспоненциального семейства распределений

Закон распределения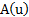
Экспоненциальный
Релея	2
Гамма
Эрланга
Вейбулла	d
Логнормальный
где Г – гамма-функция

Соответственно пик риска равен

Определяя из табл. 2.1. первые пять начальных моментов

находим:

– среднее значение ущерба

– среднеквадратическое отклонение

– центральные моменты

–ассиметрию и эксцесс кривой риска

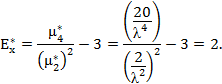
Рассчитанные параметры сведены в табл. 2.3, которую можно использовать для инженерных расчетов.

Таблица 2.3

Аналитические выражения риска и параметров (для экспоненциального распределения плотности вероятности наступления ущерба)

где: u – ущерб, – параметр распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение
Среднее значение ущерба
Мода ущерба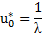
Пик риска
Среднеквадратическое отклонение ущерба
Ассиметрия риска
Островершинность риска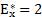

Подобную таблицу целесообразно получить для координат экстремума риска при различных законах распределения плотности вероятности ущерба.

Так, для распределения Релея на основании таблицы представляется составить уравнение

или

Решая последнее уравнение, имеем

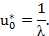
Отсюда пик риска равен

Применительно к гамма-распределению уравнение экстремума выглядит следующим образом

или

Решением такого уравнения будет мода риска

а пик риска будет равен

Далее рассмотрим распределение Эрланга, для чего составим уравнение моды

Упрощая, имеем уравнение

решением которого является мода

По аналогии составим уравнение моды для распределения Вейбула (табл. 2.2)

Упрощение уравнения приводит к виду

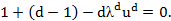
Отсюда мода равна

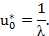
Соответственно пик риска будет равен

Применительно к логнормальному распределению плотности вероятности наступления ущерба уравнение моды риска согласно табл. 2.2 примет следующий вид

Упрощение дает

откуда находим моду риска

Соответственно пик риска будет равен

Вышеперечисленные выражения для координат экстремума риска сведены в табл. 2.4.

Теперь определим аналитические выражения параметров риска для экспоненциального распределения согласно табл. 2.2 они будут иметь следующий вид:

Таблица 2.4

Аналитические выражения моды и пика риска

Вид используемого закона распределения плотности вероятности ущерба	Мода риска	Аналитическое выражение для пика риска
Экспоненциальный
Релея
Гамма
Эрланга
Вейбулла
Логнормальный

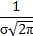
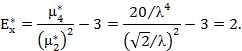
Интересно также было бы найти среднеквадратическое отклонение от моды

а также– островершинность риска на ее основе

Рассмотрим далее распределение Релея. Опираясь на выражение в табл. 2.2, имеем:

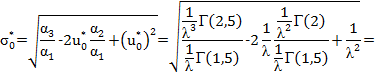
Далее не представляет труда нахождение прочих параметров

Полученные (на основе распределения Релея) параметры риска сведены в табл. 2.5 и табл. 2.6 соответственно.

Таблица 2.5

Аналитические выражения риска и его параметров (для показательного распределения плотности вероятности наступления ущерба)

Аналитическое выражение риска наступления ущерба u
где: u – ущерб, – параметр распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска
Среднее значение ущерба
Мода ущерба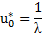
Пик риска
Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды
Островершинность риска

Таблица 2.6

Аналитические выражения риска и его параметров (для распределения Релея плотности вероятности наступления ущерба)

Аналитическое выражение риска наступления ущерба u
где: u – ущерб, – параметр распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска
Среднее значение ущерба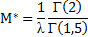
Мода ущерба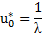
Пик риска
Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды

По аналогии для гамма-распределения найдем выражения параметров риска:

где

Полученные выражения для удобства их вычислений сведены в табл. 2.7.

Таблица 2.7

Аналитические выражения риска и его параметров (для гамма-распределения плотности вероятности наступления ущерба)

Аналитическое выражение риска наступления ущерба u
где: u – ущерб, – параметр распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска
Среднее значение ущерба
Мода ущерба
Пик риска

Продолжение табл. 2.7

Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды
Островершинность риска

Соответветсвенно для распределения плотности вероятности наступления ущерба по закону Эрланга параметры риска можно описать следующими выражениями:

Для удобства анализа, данные выражения сведены в табл. 2.8.

Таблица 2.8

Аналитические выражения риска и его параметров (для распределения плотности вероятности наступления ущерба по закону Эрланга)

Аналитическое выражение риска наступления ущерба u
где: u – ущерб, – параметры распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска
Среднее значение ущерба
Мода ущерба
Пик риска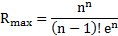
Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды
Островершинность риска

При распределении плотности вероятности наступления ущерба по закону Вейбулла параметры риска могут быть определены следующим образом:

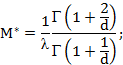
Для удобства эти и другие выражения сведены в табл. 2.9.

Таблица 2.9

Аналитические выражения риска и его параметров (для распределения плотности вероятности наступления ущерба по закону Вейбула)

Аналитическое выражение риска наступления ущерба u
где: u – ущерб, – параметры распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска

Продолжение табл. 2.9

Среднее значение ущерба
Мода ущерба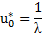
Пик риска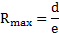
Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды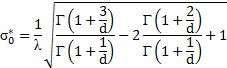
Островершинность риска

Применительно к логнормальному распределению плотности вероятности наступления ущерба могут быть получены следующие выражения параметров риска:

Эти и другие выражения сведены в табл. 2.10.

Таблица 2.10

Аналитические выражения риска и его параметров (для логнормального распределения плотности вероятности наступления ущерба)

Аналитическое выражение риска наступления ущерба u
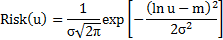где: u – ущерб, – параметры распределения плотности вероятности наступления ущерба
Наименование параметра риска	Аналитическое выражение параметра риска
Среднее значение ущерба
Мода ущерба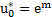
Пик риска
Среднеквадратическое отклонение ущерба
Среднеквадратическое отклонение от моды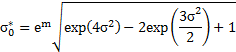
Островершинность риска

Представленные выше таблицы являются методической основой для проведения численных расчетов параметров рисков при различных законах распределения плотности вероятности наступления ущерба. Обобщенно такой алгоритм представлен на рис. 2.1.

Начало

Однако возможен и более упрощенный вариант, когда уместно ограничиться нахождением моды и среднего значения (назовем их ), а также их среднеквадратических отклонений (назовем их ). Таблицы 2.3-2.10 позволяют это сделать, а сам упрощенный алгоритм изображен на рис. 2.2.

Данные статистики наступления ущербов

Определение закона распределения и его параметров

Значения

Данные из Табл. 2.1,2.2

Расчет первых пяти начальных моментов распределения

Расчет моды и пика риска

Данные из Табл. 2.3

Значения

Рис. 2.1. Блок-схема упрощенного алгоритма расчета

параметров риска

Рис. 2.1. Блок-схема обобщенного алгоритма расчета параметров риска для компонентов систем

Расчет среднего значения ущерба

Данные из Табл. 2.3-2.10

Значение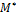

Расчет среднеквадратического отклонения ущерба

Данные из Табл. 2.3-2.10

Значение

Расчет третьего и четвертого центральных моментов

Данные из Табл. 2.3-2.10

Значения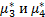

Расчет ассиметрии и эксцесса риска

Данные из Табл. 2.3-2.10

Значения

Конец

Рис. 2.1. Блок-схема упрощенного алгоритма расчета параметров риска (продолжение)

Начало

Задание вида и параметров распределения плотности вероятности ущерба

Конец

Расчет первых трех начальных компонентов распределения

Расчет среднего значения ущерба и среднеквадратического отклонения

Ввод данных в выражения Табл. 2.3-2.10

Расчет моды риска и его среднеквадратического отклонения

Вывод расчитаных значений для анализа системы

Рис. 2.2. Блок-схема упрощенного алгоритма расчета параметров риска для компонентов систем  

Воспользовавшись данными алгоритмами, можно рассчитать риск-параметры компонент системы с последующим обобщением ее анализом с учетом вклада всех компонентов. На этапе оценки риска компонента системы возможны две статегии:

– экстремальная оценка

и

– средняя оценка

Данные таблицы приемлимы не только для рисков, но и для шансов системы.

Дата добавления: 2015-10-26