Theoretical information

The motion of the body when all its points move in circles with their centers on the axis of rotation is named rotatory motion of a rigid body.

The basic kinematics characteristics of rotatory motion of a body are angular velocity 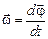and angular acceleration 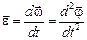, where 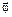is the angular displacement of a body. Vectors 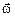and 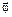have direction along rotation axis. The direction of 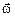is determined according to the right-hand rule.

The angular and linear characteristics are linked by relationship:

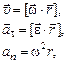
where 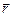is position vector of a point; is tangential acceleration of a point; 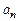is normal acceleration of a point.

Basic dynamic characteristics of rotatory motion are moment of force (torque); angular momentum and moment of inertia. Moment of force is the force analogue, angular momentum 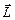is the momentum analogue, and moment of inertia I is the mass analogue.

There is connection between the moment of force and angular momentum. This connection is established by a basic equation of dynamics of rotatory motion, i.e. by the Newton’s second law of rotatory motion:

where the (vector) sum of all the torques acting on a body is equal to the time rate of change of the angular momentum of that body.

The angular momentum of a material point 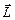rotating around immovable axis is vector product of position vector 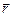and the momentum of material point

,

where I is moment of inertia of a material point.

Angular momentum of a rigid rotating body is:

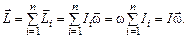
If the angular momentum of a body is constant, the law of dynamics of rotatory motion can be formulated as: an angular acceleration 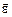is directly proportional to moment of force and inversely proportional to moment of inertia I:

.

The vector of angular acceleration coincides with direction of the vector of force moment.

A moment of force (torque) is a vector product of position vector of point of force application and vector of force:

.

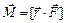The vector of moment of force is directed along the axis of rotation according to the right-hand rule: sweep the fingers of the right hand from 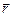(the first vector in the product) into 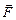(the second vector) and the outstretched right thumb then gives the direction of .

The module of momentum of force equals the product of the module of force and the shortest distance from the axis of rotation to the line of force action or the product of force on a moment arm:

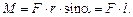
Experiments show that the change of velocity of rotatory motion, that is angular acceleration, depends not only on mass of rotating body but also on its distribution relative to axis of rotation. A quantity, which takes into account both these circumstances represents the measure of inertness in rotatory motion and is named the moment of inertia of body relative to axis of rotation.

The moment of inertia of material point relative to axis of rotation equals the product of mass of point Dm and the square of its distance r from axis of rotation:

A moment of inertia is a scalar quantity.

The moment of inertia of the whole rigid body relative to axis of rotation is equal to the sum of moments of inertia of all its elementary masses:

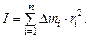
If mass is distributed continuously, this sum can be replaced by an integral:

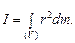
For example, the inertia moments of certain solids of regular geometrical shape about their symmetry axes are expressed by the following formulas.

1. Moment of inertia of a disk (a cylinder) with the radius of R

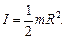
2. Moment of inertia of a rod of length l relative to the axis which passes through the middle of bar perpendicularly to its length

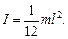
If the axis of rotation of a body is parallel to the axis of symmetry but displaced from it at distance d, moment of inertia relative to the parallel displaced axis is expressed by the Schteiner’s theorem:

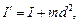
where I is a moment of inertia relative to the axis of symmetry.

To determine analytically moment of inertia of bodies of irregular form, and heterogeneous bodies as well is a difficult task, and it is sometimes impossible. That is why there is a lot of methods of inertia moments determination by an experimental way.

Дата добавления: 2015-10-26