Brief theoretical information

LABORATORY WORK № 7

ANALOG FILTERT DESIGN

BRIEF THEORETICAL INFORMATION

A filter is one, which rejects unwanted frequencies from the input signal and allows the desired frequencies to obtain the required shape of output signal.

The range of frequencies of signal that are passed through the filter is called passband and those frequencies that are blocked is called stopband.

The filters are of different types:

1. Low-pass filter (LPF). 2. High-pass filter (HPF).

3. Band-pass filter (BPF). 4. Band-stop (reject) filter (BSF).

An ideal filter will have an amplitude response that is unity (or at a fixed gain) for the frequencies of interest (called the pass band) and zero everywhere else (called the stop-band). The frequency at which the response changes from pass-band to stop-band is referred to as the cut-off frequency, . Figure 1(a) shows an idealized low-pass filter. In this filter the low frequencies are in the pass band and the higher frequencies are in the stop band. The PHF passes the high frequencies (they are in the pass band) and all the low frequencies are in the stop band (Figure 1 b – idealized HPF). If a high filter and low –pass filter are cascaded, a band pass filter is created. The BPF passes a band of frequencies berween a lower cut-off frequency, and an upper frequency, . The frequncies below and above are in the stop band. An idealized BPF is shown in Figure 1(c). The band-stop filter passes frequencies below and above . The band from to are in the stop band. Figure 1 (d) shows an idealized BSF.

Figure 1 Idealized Filter Frequency Responses

The idealized filters defined above, unfortunately, cannot be easily built. The transition from pass band to stop band will not be instantaneous, but instead there will be a transition region. Stop band attenuation will not be infinite. Practical filters are usually designed to meet a set of specifications.

To obtain a physically realizable filter, it is necessary to relax some of the requirements of the ideal filters. Figure 2 shows the frequency characteristics of physically realizable versions of various ideal filters. The upper and lower bounds for the gains are indicated by the shaded line, while examples of the frequency characteristics of physically realizable filters that satisfy the specified bounds are shown using bold lines. These filters are referred to as non-ideal or practical filters and are different from the ideal filters in the following two ways:

(a) The gains of the practical filters within the pass and stop bands are not constant but vary within the following limits:

pass bands ;

stop bands .

The oscillations within the pass and stop bands are referred to as ripples. In Figure 2, the pass band ripples are constrained to a value of 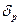for LPF, HPF, and BPF. In the case of BSF, the pass band ripples are limited to and , corresponding to the two pass band. Similarly, the stop band ripples in Figure 2 are constrained to for LPF, HPF and BSF. In the case of BSF, the stop band ripples are limited to and for the two stop bands of the BSF.

(b) Transition bands of non-zero bandwidth are included in between the pass and stop bands of the practical filters. Consequently, the discontinuity at the cut-off frequency of the ideal filters is eliminated.

Дата добавления: 2015-10-28