Standard task for laboratory work

1. Define transfer function of Butterworth low pass filter of the n-th order with cut-off frequency . Values for cut-off frequency and filter order are given in Table 1.

Table 1

BUTTERWORTH LOW PASS CHARACTERISTICS

Variants
ωс, rad/s	0.25		1·10^3		0.75	0.85
n, order

2. A Butterworth low pass filter is given by magnitude response function

.

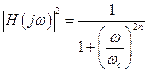Define an order of Butterworth low pass filter that satisfies the following requirements (see eq. 4)

a) maximum attenuation in pass band, R_p=1 dB;

b) pass band frequency is equal to 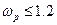rad/s;

c) stop band frequency, 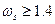rad/s;

d) attenuation in stop band, R_s=40 dB.

3. Define a magnitude frequency response of low pass Chebyshev filter of the n-th order if the pass band is equal to 1 rad/s and pass band ripple, δ is equal to 0.5. The order of the filter is given in Table 2.

Table 2

CHEBYSHEV FILTER ORDER

Variants
n, order
Variants
n, order

4. Construct an analog low pass Butterworth filter within Simulink environment and investigate its properties. The filter structure is shown in Figure 4.

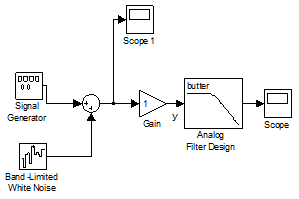
Figure 4 Analog Filter Design

Take the block for analog filter simulationfrom Signal Processing Blockset\ Filtering\Filter Designs\ Analog Filter Design

Define Main properties for low pass Butterworth filter:

· Design method – Butterworth Filter;

· Filter type – low pass;

· Filter order – 2.

To generate a harmonic signal use Signal Generator block from Simulink\Sources Library. Open Signal Generator block parameters and define the following parameters

· Wave form;

· Amplitude и Frequency;

· Units – set units to rad/sec.

Type of the harmonic signal is given below by y.

a) Generate a signal that has the following form

y = K ₀ · 2 · sinω +noise,

where the sine wave frequency is equal to ω=20 rad/sec. Apply the filtering via Butterworth filter.

b) Generate a signal than involves a low period and high period components, respectively. Hence, the signal y takes the following form

y = K _0· · (2 · sinω₁ +2 · sinω₂),

with ω₁=20 rad/sec and ω₂=80 rad/sec.

Apply the simulation according to individual variants (see Table 3): Butterworth approximation, cut-off frequency ω_с; gain K₀. Set the simulation time to 5.

Table 3

INITIAL DATA FOR ANALOG FILTER DESIGN

Varian
ωс, rad/sec
K0

Дата добавления: 2015-10-28