Estimation rules of direct measurement random error

The question is: what value of unknown quantity can be taken as a true value and how can the measurement error be estimated? Random error theory based on the mathematical apparatus of probability theory can give the answer to this question. The probability theory gives certain regularities in the casual quantities behavior. If we cannot preliminarily say, what value of casual quantity will appear at next measurement, then at a quite enough number of measurements we can surely foresee, how many times this or that value will appear. So, there is a well-defined probability of a certain casual event. The probability theory enables to determine this probability.

What is understood under probability of a random event?

Probability of a random event P (A)is the limit when the total amount of cases (n) becomes infinite to the ratio between amounts of cases, when this event takes place , and the total amount of cases is:

.

Probability of appearance of the measured physical quantity value during quite great number of measurements is different.

Let us determine how many times this or that value has appeared during measurement. First of all we are to arrange the obtained values in increasing progression starting from x ₁ up to x_n (where x ₁ is the smallest value of quantity x _i, x _n is the peak value) and we are to divide the whole range of obtained values into k equal intervals of width .

The magnitude of each interval is determined as follows

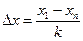
Now it is possible to determine a number of values within intervals Dn₁, D n ₂,… D n _k and calculate frequency of

the measured values appearance in each of intervals D n ₁/ n, D n₂ / n,… D n _k/ n. Knowing the distribution of random values, we can draw a diagram (fig. 1). Interval magnitude D x ₁, D x ₂,… D x_k is put on the abscissa axis and appearance frequency of measured values within the corresponding interval is put on the ordinate axis. Such a diagram is named a histogram.

Thus, we found out, that some values of x_i appeared more often than others, and that the probability of appearance of different values of x_i is different. If the number of values approaches infinity and interval magnitude tends to be zero, the upper sides of rectangles form a continuous curve. This curve and its function are named distribution curve and distribution function f(x). A typical curve of random distribution is shown in Fig. 2. Distribution function value demonstrates that the product f(x)dx determines the part of measurements n within an interval from x to x+dx. This part is graphically represented as the shaded rectangle area (fig. 2). As a sum of all parts equals unity, the sum of all rectangles, that is the whole area under the curve of distribution, equals unity. Thus, according to the distribution curve it is possible to determine the probability of the measured quantity appearance from the value x to .

The distribution curve has a maximum. It means that at a quite great number of measurements, values appearance corresponding to the abscissa maximum has the most probability. Otherwise, the value is the most probable value of the measured quantity. The distribution curve of the measured quantity is symmetric in relation to this value. It is possible to deduce that at a quite great number of measurements; the value tends to the true value of the measured quantity, that is, ® X at n® ¥. If the true value of the measured quantity is known, it is possible to calculate the errors of the separate measurements as

As the appearance of this or that value x_i during measurement is a random event, the appearance of this or that value of error is a random event too.

Probability of such an event is also described by the distribution function . It can be obtained from the considered distribution function subtracting value from x_i that it is to carry the origin in point (fig. 3).

Examining this curve, it is possible to establish:

1) errors of different signs, but of the identical modulus are met equally often, because the distribution curve is symmetric in relation to the ordinate axis;

2) errors of large modulus are met more seldom because the distribution curve falls with increase .

These two experimental facts can be used for estimating analytical expression of the distribution curve. We only need to add . The analytical expression of the distribution function received by German mathematician Gauss looks like

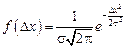
where is an error of the separate measurement; е is a basis of natural logarithm; 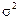is a constant value named dispersion.

Gaussian distribution law is often named the normal distribution law. Figure 4 represents Gaussian distribution function for three values of dispersion. The less value of dispersion, the faster Gaussian distribution falls to abscissa axis. It means that errors with small modulus prevail.

What errors and how is dispersion concerned with? Assume that we have conducted n measurements of certain quantity x and have a set of values 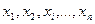. Then, as it is known from the probability theory, the most probable value is taken as an arithmetic meanof all measured values:

A root-mean-square error of separate measurementsis equal to:

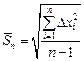
where is random deviation of every measured value from a mean value.

At infinitely large number of measurements the arithmetic mean equals the true value of the measured quantity, and root-mean-square error of the separate measurementequals the dispersions:

; .

Consequently, dispersion is referred to the errors of measurements.

In practice it is necessary to know the probability of the errors of measurements not to exceed some preliminary values, for example . If the dispersion of measurement method is known, it is possible to build Gaussian distribution curve and then using obtained curve to define this probability. For this purpose will plot two lines parallel to ordinate axis which passes through values and . (fig.5).

The shaded area, which is between the plotted two lines, abscise axis and Gaussian distribution curve, will be equal to probability that the absolute value of measurements error does not exceed value . The less the value the less the shaded area, and error appearance probability value from 0 to reduces. Table 1 demonstrates this probability for some error values . The error value is taken in a scale of , it is convenient for comparing different errors probabilities.

Table 1

Error value,	0,1s	0,5s	0,675s	s	2s	3s
Probability a of error appearance from 0 to	0,080	0,383	0,500	0,683	0,954	0,997

From table 1 it follows, that if we perform 1000 experiments according to the method with dispersion of σ², the error will be less than or equal to 0,1s approximately in 80 experiments; the error will be less than or equal to s approximately in 683 cases; the error will be less than or equal to 2s in 954 experiments and it will be bigger than 3only in three measurements.When we say probability of error appearance is equal to 0,954, in this case the error does not exceed the value 2s with the given probability. Then

or .

It means that the true value of measured value can differ from measured no more than 2s, or the true value is in interval from to with probability .

If we choose other interval, another probability will appear. For example, if the true value of the measured value will be in interval from to with probability only 0,683.

So, the less random error , the less the probability of measured true value is in an interval from to .

Thus, random erroris characterized by both error module and corresponding probability.

The interval from to is named confidence interval, and probability of the fact that real value of the measured value in this interval is called confidence probability or reliability. It is denoted by a.

Thus, to describe a random error it is necessary to set confidence interval and confidence probability. Setting this or that confidence probability the corresponding confidence interval can be found.

In most cases confidence probability value equal to 0,95 is used, that is why considering concrete problems of error calculation we take a = 0,95, it means that up to 5% measured values cannot be in confidence interval.

However, in practice number of measurements is never infinitely large and the arithmetic mean will not be equal to the true value of measured value. What can we do in this case? At the limited amount of measurements the arithmetic mean would be nearly the true value of the measured value.

A difference between a single result of observation and arithmetic mean is named, as it was mentioned above, the casual deviation of observation result, and arithmetic mean is called mean value.

What is the mistake in of error of arithmetic mean determination? It also enables to establish the casual values theory. As in the probability theory, error of arithmetic mean is

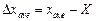
It is a casual value which distribution is described by Gaussian distribution function with dispersion . Dispersion of mean value has relationship with dispersion for the error of the separate measurement

,

That arithmetic mean dispersion depends on the amount of measurements n and it reduces when n increases. Table 1 enables us to estimate confidence probability of value x_ave, if another value will be taken instead of s:

.

For example, probability is equal to 0,954. Therefore

or in other form

.

At the limited amount of measurements, close value of dispersion of arithmetic mean is:

.

At a big number of measurements

.

Square root from value is named the root-mean-square error of the arithmetic mean

.

The value is usually named the root-mean-square error of the measurements result. As was mentioned above, the measurements amount is limited and seldom exceeds 10. Then the less measurements amount, the bigger is the difference between the root-mean-square error and dispersion. So, if the confidence probability decreases the confidence interval increases.

The probability theory solves this problem too.

The problem of change of width confidence interval as the result of series of measurements depending on the amount of measurements was solved by English mathematician Goset in 1908, who published the works under the pseudonym «Student». Goset received the distribution function for a correction factor t_st. To obtain the confidence interval at a given confidence probability it is necessary to multiply the root-mean-square error of arithmetic mean bycorrection factor. This coefficient is named the Student’s coefficient. The Student’s coefficient depends on both number of measurements n and confidence probability a. Table 2 gives the value of Student’s coefficient for different amounts of measurements and for different values of confidence probability.

Table 2

n	a
0,90	0,95	0,99
Student’s coefficient, tst
	6,31	12,70	63,70
	2,92	4,30	9,92
	2,35	3,18	5,84
	2,13	2,78	4,60
	2,02	2,57	4,03
	1,94	2,45	3,71
	1,89	2,36	3,50
	1,86	2,31	3,36
	1,83	2,26	3,25

So, random error of direct measurements equals the half-width of confidence interval:

.

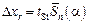The measurements results are given in a form:

.

Confidence probability, which was taken during the calculation of random error, is specified in parenthesis after its value.

---

Дата добавления: 2015-10-26