Work procedure and data processing

1. Put the Atvud’s machine on the table using three screws in the basis of the machine.

2. The right load of the machine must be in the center of support 1, placed on a bottom position.

3. The time intervals are measured by a stop watch.

Task 1. Condition v = const examination

The student should do the following:

1. Put load 7 on the right load. Lock the electromagnet circle. The system is in an equilibrium state. Put the support 1 under the load in the 10 sm distance from the top end of the leg. Put the support 4 under the load in the 60 sm distance from the top end of the leg.

2. Unlock the electromagnet circle. Measure the time of the load motion between the support 1 and support 4. Repeat measurement 3 times.

3. Measure distance between supports.

4. Without changing the position of the support 1, lift support 4 to 5 sm distance and repeat measurements according items 2, 3. Enter the results into the table 1.

Table 1

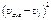
No	h, m	t, s	v, m/s			Note
Mean value	—

5. Carry out measurements at 5 different positions of support 4.

6. Knowing distance between supports and height of the right load, determine the velocity of uniform motion between supports:

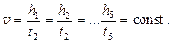
7. Calculate the absolute and fractional errors of time measurement.

8. Calculate the absolute error of velocity measurement:

.

9. Calculate the fractional error of velocity measurement:

10. Write down the obtained results in a form:

11. Plot the graph as the dependence . Analyze the obtained graph.

Task 2. Speed law examination

The student should do the following:

1. Put load 7 on a right load. Lock the electromagnet circle. The system will be in an equilibrium state. Put the support 1 under the load in the 10 sm distance from the top end of the lag. Put the support 4 under the load in the 60 sm distance from the top end of the leg.

2. Unlock the electromagnet circle. Measure time of load motion t₁ from initial position to the support 1 andtime of load motion between the support 1 and support 4. Repeat measurements 3 times. Enter the results into the table 2.

3. Measure distance between supports.

4. Return the system into the initial position. Change position of support 1, and repeat measurements according to items 2, 3. Carry out measurements at 5 different positions of support 1. Enter the results into the table 2.

Table 2

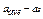
No	h, m	t, s	, s	v, m/s	, m/s^2			Note
Mean value	—		—	—

5. If the distance between the right load and support 1 changes the velocity of the load between the supports changes too. Acceleration of the system will be constant if the loads have the same mass:

.

6. The velocity of uniform load motion between supports equals the instantaneous velocity of uniformly accelerated motion in the time moment of t₁. Then the acceleration of the system may be determined as:

.

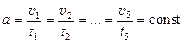7. Calculate absolute and fractional errors of time measurement.

8. Calculate the absolute error of acceleration measurement:

.

9. Calculate fractional errors of acceleration measurement:

%.

10. Write down the obtained results in a form:

.

11. Plot the graph of the dependence . Analyze the obtained graph.

Task 3. Displacement law examination

1. Put load 6 with mass m₁ on the right load. Switch on the current in electromagnet circle and set the system so that the left load remains immovable under the electromagnet action.

2. Set support 4 at the certain distance h from the bottom basis of the right load. Unlock the electromagnet circle, and start a stop watch.

3. Stop a stop watch at the moment when the right load reaches the support 4. It is the time of load motion t. Repeat measurements 3 times.

4. Measure distance h. Enter the results into the table 3.

Table 3

No	h, m	t, s	а, m/s^2	a т, m/s^2	Note
					m = m 1 = g = 9,8 m/s^2
Mean value

5. Measure time t according to items 2 – 4 for the same mass of loads 6having changed the value of h.

6. Carry out measurements at 5 different positions of support 4. Enter the results into the table 3.

7. The acceleration of the system in all cases will be the same. Then

.

8. Calculate the theoretical value of acceleration of the system by a formula (4).

9. Calculate absolute error as:

.

10. Calculate fractional error as:

%.

11. Write down the obtained results in a form:

.

12. Plot the graph of the dependence . Analyze the obtained graph.

Task 4. The Newton’s second law 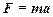examination

The student should do the following:

1. Replace the load from the right position into the left one. Then the resulting external force applied to the system and its acceleration change. Mass of the system remains constant.

2. For two different cases we have:

.

Therefore:

.

Dividing equation will be:

.

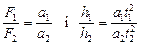Thus

. (5)

This equality needs to be checked.

3. Putting the load 6 on the right support, lock the electromagnet circle.

4. External force of F_i, applied to the system, equals the difference between the right and the left loads.

5. Place support 4 at the certain distance h_i from a right load.

6. Unlock the electromagnet circle. Measure the time interval t_i from the start of a system motion to the moment when the right load reaches support 4.. Enter the results into the table 4.

Table 4

No	h 1, m	h 2, m	t 1, s	t 2, s		Note
Mean value

7. Carry out measurements 5 times for the different amounts of loads.

8. Check up the relationship (5):

.

9. Make conclusions.

questions to be admitted for doing laboratory work and its defence

1. What does mechanics study? What parts of mechanics do you know?

2. What does kinematics study?

3. Enumerate basic kinematics characteristics of translational motion.

4. What does dynamics study?

5. Enumerate dynamic characteristics of translational motion. Write down the corresponding formulas and measurement units.

6. Formulate the Newton‘s first law.

7. Formulate the Newton‘s second law. Write down it in a general vector form.

8. Formulate the Newton’s third law. Write down it in a vector form.

9. Describe the method of acceleration determination with the Atvud’s machine.

10. How can you calculate a rope tension in Atvud’s machine at uniform and uniformly accelerated motions of the system of bodies?

LABORATORY WORK

Liquid viscosity coefficient determination

The purpose of the work: to study the transport phenomena of transference; to determine the internal friction coefficient by the Stock’s method.

Theoretical information

A system being initially in a non-equilibrium state (this implies that a certain thermodynamics parameter has different values in different parts of the system) tends to pass spontaneously to the equilibrium state (each thermodynamics parameter becomes the same in any part of the system). Non-equilibrium state of a system is characterized by different densities or temperatures in different parts of the system, and by different speeds of directed motion of gas or liquid layers as well.

Let’s assume that a non-equilibrium state of a system refers to different densities (or concentrations) in different parts of the volume. In such a system irreversible process takes place and the concentration of particles becomes the same throughout the volume and the system passes to the state of equilibrium. The process of density equalization refers to mass transport, and the requirement for the observed phenomenon consists in the initial difference in particles concentration in different parts of the system. The phenomenon of mass transport from the zone of higher concentration of particles to one of lower concentration is called diffusion.

Fig. 1

Let us consider a case when temperature in different parts of a body is not equal. For example, a metal bar the left end of which is heated and the right end has a lower temperature. A temperature gradient exists along the rod. The process of temperature equalization takes place. The process is accompanied by transmission of internal energy and is called thermal conductivity.

Whenever a liquid (or gas) flows, the velocities of different layers are different and increase with the distance from the fixed surface. A velocity gradient exists along the z-axis. If any two layers are considered, the layer having a higher speed tends to accelerate the motion of the slower layer, and the latter tends to retard the motion of the faster layer. The two layers together tend to destroy their relative motion, as there is a backward dragging tangential force This property due to which a liquid (or gas) opposes the relative motion of different layers is called viscosity or internal friction The internal friction refers to transport of particles' momentum.

Hence, three phenomena – diffusion, thermal conductivity and internal friction – have the similar mechanism – equalization of heterogeneities, which exists in different parts of the system (in case of diffusion, it is concentration equalization; in heat conductivity – temperature equalization; and in case of internal friction – speed equalization). We need similar conditions to observe each of these phenomena – concentration, temperature or speed gradient. And three phenomena are accompanied by transfer of particles characteristics – mass, energy or momentum.

When a liquid (or gas) flows slowly and steadily through a pipe, the liquid layer close to the pipe is practically stable, but the central part of the liquid is moving relatively fast. Other liquid layers have velocities less than that of the central layer. Now as in the case of two solid surfaces moving over each other, frictional force acts between two liquid layers when they move over each other. Thus, as the velocities of adjacent layers are different (Fig.1), frictional force occurs between the various liquid layers flowing through a pipe.

The basic formula for the frictional force, F, in a liquid was at first suggested by Newton. He saw the larger considered liquid surface area S, the greater was the frictional force. He also stated the force was directly proportional to the velocity gradient at tin part of the considered liquid. These most common liquids are called Newtonian liquids. Thus, the frictional force on the surface is expressed as:

. (1)

where is a constant of liquid known as dynamic viscosity coefficient (internal friction coefficient), it numerically equals the force of friction between two layers, which contact area equals one for a unit velocity gradient. The negative sign shows that the direction of force is opposite to the direction of velocity. This formula is known as Newton-Stock law for internal friction. (Quantity is called fluidity)

Measurement unit is expressed in [kg/m·s]. The velocity gradient d /dz characterizes the change of layers motion velocity for a length unit directed along the normal to the velocity of layers motion.

Quantity is called kinematics viscosity coefficient, where ρ is liquid density.

The coefficient of dynamic viscosity depends on nature of liquid. The temperature of a liquid being raised, the coefficient decreases with temperature according to the exponential law:

,

where h_o is a coefficient independent on temperature;

k = 1.38 is Boltzmann’s constant;

U is energy of a molecule needed to change its place.

There is a general formula for determination of the coefficient

,

where is a mean velocity of molecules;

l is amean free path of molecules;

is a density of liquid.

There are many ways to determine the coefficient experimentally. Stock’s method is the most popular among them. It is based on the speed of a small ball dropped into a liquid.

Measurement procedure and experimental equipment

The device is a high thin transparent cylinder filled with investigated liquid (fig.2). At the top of the cylinder, there is a lid with a cover with an opening. We drop a small-shot ball and observe its motion. It is not difficult to calculate the speed of the ball.

Fig. 2

Let’s consider a ball dropped in viscous liquid. Three forces make the ball move (Fig.2):

1) the gravity force:

(2)

where V is the volume of a ball; r is the density of a ball; g is gravity acceleration;

2) the Archimedes force

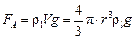(3)

where r _l is the liquid density in the cylinder;

3) the force of internal friction F

(4)

where h is internal friction coefficient; r is the radius of a ball; u is the speed of a ball.

According to the second Newton’s law we get

. (5)

The speed of the ball being raised the force of internal friction increases and the acceleration of the ball slows down to zero. So the equation (5) for a steady motion of a ball looks like

Substitute P, and F by their equations (2), (3), (4)

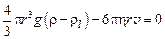. (6)

Deduce the equation (6)

.

where (l is the distance between the scores; t is the time a ball passes this distance).

Finally:

(7)

We must also know the radius of a ball, the densities of ball and liquid, and the time a ball passes the distance l.

---

Дата добавления: 2015-10-26