Indirect measurement error estimation rules

In most cases unknown value of physical quantity is not measured directly. The required quantity is calculated by the dependence between this quantity and that one determined by direct measurements. The errors of directly measured quantities are known as well.

The general rules of indirect measurement errors evaluation can be obtained only by means of the errors mathematical theory and differential calculus methods. In this work, we consider the error calculation formulas and their application.

Let the required quantity y depends on few values х_і, which are measured directly and independently. Dependence y on х_і isknown:

, (1)

and absolute error under the identical value of confidence probability a is determined for each directly measured quantity. Then the absolute error of indirect measurements is defined by the expression:

, (2)

where, and so on are partial derivatives of function in respect to separate independent variables , and so on.

Sometimes indirect measurements errors calculation is more convenient to begin with fractional error calculation. Thus, simpler expressions of fractional errors are used.

Measured indirectly fractional error of quantity is defined as follows .

Then from a formula (2) it follows:

.

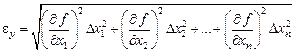Accordance to differentiation rules, we have:

Thus, expression for fractional error of indirect measurements looks as follows:

. (3)

Expression (3) includes partial derivatives of function logarithm instead of partial derivatives of function f (x).

Formula (3) is more convenient for the function application:

, (4)

where A, l, m., к are constant values, which can be integer or fraction, positive or negative.

Having obtained the formula of indirect measurements error, we determine the value of indirectly measured quantity For this purpose, mean values of directly measured quantities are used. An absolute error is calculated as follows:

.

The measurements final result is expressed by:

.

The required quantity measurement error has the same confidence probability as the direct measurements.

Part І. Solid Body Density Determination

In this work, density of a cylinder standard is determined as a result of measurements of its parameters: height h, diameter d and mass m.

Density of homogeneous body is the ratio between its mass and its volume: or, otherwise, density is determined as mass of a unit volume.

Mass is the measure of inert and gravitational properties of a body. It is a scalar and additive physical quantity.

Volume of a cylinder sample is:

Then density of cylinder standard is determined according to a formula:

. (5)

Having written this formula as the expression for fractional error determination will be obtained.

Take the logarithm of the expression:

.

Calculate partial derivatives taken in respect to m, d and h:

; ; .

Putting these partial derivatives values in equation (3), we will obtain the formula for the fractional error calculation:

(6)

Having calculated the fractional error , we get the absolute error:

(7)

The final result of the indirect measurements is expressed as follows:

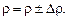
Дата добавления: 2015-10-26