Приклад розв’язання контрольних завдань

Для множин знайти.

Спростити вираз.

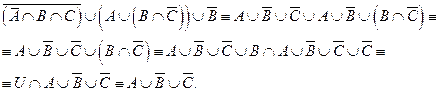
Дано множини:.

Знайти ;

Знайти потужності кожної з множин;

Для рівнопотужних множин задати бієкції однієї множини на іншу.

;

;

Запишемо множину раціональних чисел у вигляді таблиці:

Множини 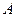та рівно потужні, тому задамо бієкцію цих множин:

Для логічної формули :

Скласти табличку істинності;

Спростити формулу за допомогою рівносильних перетворень;

Знайти ДДНФ;

Знайти мінімальну ДНФ.

Скласти табличку істинності:

Спростити формулу за допомогою рівносильних перетворень:

Знайти ДДНФ:

Знайти мінімальну ДНФ:

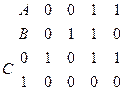
Мінімальна ДНФ .

З’ясувати, чи утворює групу множина цілих чисел відносно додавання.

0 – нейтральний елемент, ;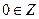

Для будь-якого 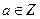існує симетричний елемент .

Довести методом математичної індукції, що.

При , ;

Нехай рівність виконується при ;

Доведемо, що вона виконується при ;

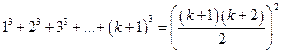
Скільки слів можна утворити, переставляючи букви слова „МНОЖИНИ”.

В цьому слові є повторні входження букв, тому скористаємось формулою для перестановок із повторенням:

.

Питання до заліку

Булеві функції: основні поняття та означення; способи задання; область визначення.

Елементарні функції алгебри логіки, їхні властивості.

Реалізація булевих функцій формулами. Поняття формули, принцип суперпозиції, рівносильність формул.

Основні тотожності алгебри логіки.

Принцип двоїстості в логіці.

Предикати. Квантори. Формули логіки предикатів. Рівносильність формул.

Числення формул предикатів.

Множина: основні поняття та означення. Способи задання множин. Порожня та універсальна множини.

Алгебра множин.

Потужність множини.

Поняття та основні властивості відношень.

Відношення еквівалентності, порядку, рівнопотужності.

Алгебраїчні системи: основні поняття, означення та властивості.

Гомоморфізм та ізоморфізм алгебр.

Види алгебр з однією алгебраїчною операцією: півгрупа, група.

Алгебри з двома алгебраїчними операціями: кільце, поле

Набори повних функцій.

Теореми Жегалкіна та Поста.

Диз’юнктивна та кон’юнктивна нормальна форми перемикальних функцій.

Досконала диз’юнктивна та кон’юнктивна нормальна форма.

Мінімальна диз’юнктивна та кон’юнктивна нормальна форма.

Скорочена диз’юнктивна та кон’юнктивна нормальна форма.

Метод Клайна-Маккласкі.

Тупикові нормальні форми.

Утворення мінімізаційних кон’юнктивних нормальних форм (діаграми Карно-Вейча, метод Блейка-Порецікого).

Поняття формальної системи. Аксіоматичний спосіб опису висловлювання. Властивості числення висловлень. Повнота і несуперечливість числення висловлень. Незалежність аксіом.

Питання до екзамену

Булеві функції: основні поняття та означення; способи задання; область визначення.

Елементарні функції алгебри логіки, їхні властивості.

Реалізація булевих функцій формулами. Поняття формули, принцип суперпозиції, рівносильність формул.

Основні тотожності алгебри логіки.

Принцип двоїстості в логіці.

Предикати. Квантори. Формули логіки предикатів. Рівносильність формул.

Числення формул предикатів.

Множина: основні поняття та означення. Способи задання множин. Порожня та універсальна множини.

Алгебра множин.

Потужність множини.

Поняття та основні властивості відношень.

Відношення еквівалентності, порядку, рівнопотужності.

Алгебраїчні системи: основні поняття, означення та властивості.

Гомоморфізм та ізоморфізм алгебр.

Види алгебр з однією алгебраїчною операцією: півгрупа, група.

Алгебри з двома алгебраїчними операціями: кільце, поле

Метод математичної індукції.

Основні закони комбінаторики (правило суми і добутку).

Основні формули комбінаторики: розміщення, сполуки, перестановки з повтореннями і без повторення.

Трикутник Паскаля. Біном Ньютона.

Основні поняття теорії графів.

Задання графа за допомогою матриць інцедентності та суміжності.

Локальні степені вершин та ребер графа.

Маршрути, ланцюги та цикли. Зв’язність графа. Дерева.

Ейлерові та Гамільтонові графи.

Набори повних функцій.

Теореми Жегалкіна та Поста.

Диз’юнктивна та кон’юнктивна нормальна форми перемикальних функцій.

Досконала диз’юнктивна та кон’юнктивна нормальна форма.

Мінімальна диз’юнктивна та кон’юнктивна нормальна форма.

Скорочена диз’юнктивна та кон’юнктивна нормальна форма.

Метод Клайна-Маккласкі.

Тупикові нормальні форми.

Утворення мінімізаційних кон’юнктивних нормальних форм (діаграми Карно-Вейча, метод Блейка-Порецікого).

Поняття формальної системи. Аксіоматичний спосіб опису висловлювання. Властивості числення висловлень. Повнота і несуперечливість числення висловлень. Незалежність аксіом.

Канонічна система Поста. Машина Тьюрінга як окремий випадок канонічної системи Поста. Використання канонічних систем Поста і машин Тьюрінга.

Основні поняття і властивості алгоритмів. Рекурсивні функції: примітивно-рекурсивні, частково-рекурсивні, теза Черча. Машини Тьюрінга. Зв’язок рекурсивних функцій з машинами Тьюрінга.

Нормальний алгоритм Маркова. Загальна теорія алгоритмів. Прикладна теорія алгоритмів. Теорема Райса.

Розв’язання комбінаторних задач методом Пойя: реалізація групи, дія групи на множині.

Орбіти. Лема Бернсайда про кількість робіт. Застосування леми Бернсайда для розв’язання комбінаторних задач.

Частини графа, суграфи та підграфи. Операції з частинами графа. Графи та бінарні відношення.

Чикломатичне число графа. Хроматичне число графа.

Кістякове дерево зв’язного графа. Мінімальні кістякові дерева зважених графів.

Планарність графів. Проблема чотирьох фар: постановка задачі, двоїстий граф, конфігурації, що редрукуються, породження плоских графів. Теорема Ейлера про многогранники.

Екстремальні задачі в теорії графів. Булеві матриці. Вилучення компонент зв’язності.

Задачі пошуку маршрутів у графі. Пошук відстані між вершинами графа. Мінімальні шляхи у зважених орієнтованих та неорієнтованих графах.

Гамільтонові ланцюги та цикли у зважених графах.

Список рекомендованої літератури

Бардачов Ю.М., Соколова Н.А., Ходоков В.Є. Дискретна математика. – К.: Вища школа, 2002. – 288 с.

Бондаренко М.Ф., Білоус Н.В., Руткас А.Г. Компютерна дискретна математика. – Харків: компанія СМІТ, 2004. – 480 с.

Донской В.Л. Дискретная математика. – Симферополь: Сонат, 2000. – 360 с.

Нікольский Ю.В., Пасічник В.В., Щербина Ю.М. Дискретна математика. – К.: Видавнича група ВНV, 2006. – 368 с.

Новиков Ф.А. Дискретна математика для програмистов. – С. – Пб.: Питер, 2002.- 304 с.

Про автора

Демченко Олена Олександрівна – викладач Черкаського державного бізнес-коледжу. Закінчила математичний факультет Черкаського національного університету (2005 р.).

Навчальне видання

ДЕМЧЕНКО Олена Олександрівна

Дискретна математика

Методичні рекомендації

для студентів заочної форми навчання

Редактор А.М. Азьмук

Коректор І.М. Прозоровська

Комп’ютерний набір О.О. Демченко

Підписано до друку 06.12.06. Формат 60х84¹/₁₆

Папір офсет. Гарнітура Times New Roman. Друк офсетний.

Умов. друк. арк. 0,66. Тираж прим. ____ Зам. № 69

Видавництво ТОВ „Інтеграл-техноімпекс”

18000, м. Черкаси, вул. Смілянська, 2

За довідками з питань реалізації

звертатись за тел. [phone]

Дата добавления: 2015-10-26