Соотношение Эйнштейна

(3.1.15)

аналогично для дырок

(3.1.15*)

Два последних неравенства известны как соотношения Эйнштейна и применимы для равновесного и неравновесного состояния.

Эффект Холла

Рассмотрим ток, протекающий в бруске из некоторого материала.

E

B

I

Правило правой руки

Если поместить брусок в постоянное магнитное поле, то сила, действующая на электрон со стороны этого поля, равна: . Поэтому электроны будут отклоняться вверх и там накапливаться. В результате между нижним слоем положительных и верхним слоем отрицательных зарядов появится электрическое поле. Это внутреннее поле через некоторое время прекратит движение электронов вверх, т.е. установится равновесие, при котором сила, действующая на электрон со стороны магнитного поля, уравновешивается силой со стороны электрического поля. Это произойдет при:

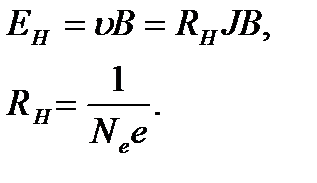
- постоянная Холла. Точнее:

- фактор Холла.

В подобных экспериментах и легко измерить, поэтому постоянную (а, следовательно, и ) можно легко определить.

Следствия:

1. можно определить полярность зарядов (дырки или электроны);
2. можно определить подвижность, проводя измерения удельной проводимости и эффекта Холла.

35,37. Механизмы рассеяния носителей тока. Зависимость подвижности от температуры.

Изменение состояния электронов вследствие их взаимодействия с отклонениями от периодичности поля кристаллической решетки называют процессом рассеяния электронов и дырок.

В классической физике изменение состояния можно трактовать как искривление траектории движущегося электрона. В квантовой – переход из одного места в зоне Бриллюэна в другое.

Различают следующие основные механизмы рассеяния носителей заряда:

1) на тепловых колебаниях решетки.

2) на дефектах решетки.

3) на носителях заряда.

Последним механизмом рассеяния, как правило, в теории полупроводников пренебрегают. Поэтому рассмотрим кратко два первых.

Рассеяние на тепловых колебаниях решетки должно быть прямо пропорционально поперечному сечению того объёма, который занимает колеблющийся атом. Это поперечное сечение прямо пропорционально квадрату амплитуды колебаний атомов.

Но квадрат амплитуды тепловых колебаний частицы, которому пропорциональна средняя энергия ее теплового движения, пропорционален температуре 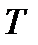. Следовательно, рассеяние, характеризуется коэффициентом рассеяния , прямо пропорционально температуре.

Длина свободного пробега .

Средняя скорость теплового движения носителей заряда в невырожденных полупроводниках .

Учитывая, что согласно (3.1.2)

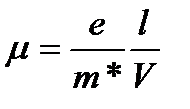
(3.3.1)

т.е. с ростом температуры подвижность, обусловленная рассеянием на тепловых колебаниях решетки, уменьшается. Это очевидно: чем выше температура, тем интенсивнее тепловые колебания решетки, тем больше флуктуации периодического поля решетки, уменьшается. Это очевидно: чем выше температура, тем интенсивнее тепловые колебания ионов решетки и больше вероятность рассеяния носителей заряда, ограничивающих их подвижность.

Среди дефектов наибольшее влияние на рассеяние тока оказывают ионы примесей. Для этого механизма рассеяния характерно уменьшение эффективности рассеяния движущегося заряда при увеличении скорости движения. Так как с возрастанием скорости уменьшается время воздействия центров рассеяния на движущиеся заряды. Вследствие этого длина свободного носителя растёт с увеличением скорости по закону , а подвижность т.к. , то

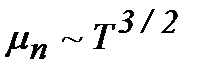(3.3.2)

т.е. подвижность носителей заряда при рассеянии на ионизированных примесях растёт пропорционально . Этот механизм рассеяния преобладает над первым при низких температурах.

Если в рассеянии носителей заряда участвуют оба рассмотренных механизма рассеяния и они независимы, то температурная зависимость подвижности носителей можно представить в виде

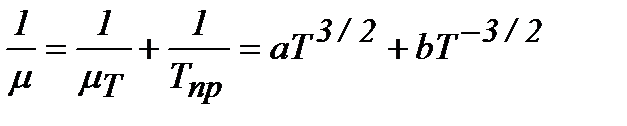(3.3.3)

где 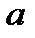и - коэффициенты пропорциональности, независящие от .

Из (3.3.3) (3.3.4)

Из последнего выражения видно, что при достаточно низких токах, когда незначительно по сравнению с их рассеянием на ионизированных примесях, подвижность возрастает с повышением температуры.

При достаточно высоких температурах убывает с ростом температуры.

Температуру, соответствующую максимальному значению подвижности, можно найти из условия .

Она равна .

Заметим, что подвижность сравнительно слабо зависит от температуры – по дробно степенному закону и не может обеспечить столь сильную экспоненциальную зависимость электропроводности от температуры, какая наблюдается на опыте. Более того, при достаточно высокой температуре падает с ростом , тогда как электропроводность сильно растёт. Следовательно, фактором, оказывающим решающее влияние на электропроводность полупроводника и её зависимость от температуры, является концентрация, а не подвижность.

Рассеяние носителей заряда на нейтральных примесях не зависит от температуры, ни от энергии носителей. Это обусловлено тем, что для того, что для того, чтобы электрон изменил направление своего движения, в результате взаимодействия с нейтральным дефектом необходим акт столкновения в буквальном смысле этого слова, то есть траектория электрона должна проходить через место расположения дефекта.

Однако при очень низких температурах, когда тепловые колебания решётки не играют заметной роли и степень ионизирующей примеси ещё мала, изменения подвижности могут быть обусловлены изменением эффективной массы носителей заряда. Простейшей причиной этого явления тепловое расширение решётки.

Подвижность электронов и дырок зависит от концентрации примесей. С ростом концентрации примеси подвижность электронов и дырок уменьшается.

---

Дата добавления: 2015-10-31