Адиабатическое приближение (приближение Борна - Оппенгеймера).

В его основе лежит тот факт, что масса ядер много больше, чем масса электронов (даже если бы кристалл состоял из самых легких атомов – атомов водорода, то 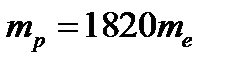). В равновесном состоянии средние значения кинетической энергии тех и других частиц одного порядка. Поэтому скорости движения электронов намного превосходят скорости ядер (). При каждом изменении положения ядер практически мгновенно устанавливается пространственное распределение электронов, соответствующее новому положению ядер. Это позволяет в первом приближении рассматривать движение электронов в потенциальном поле фиксированных ядер. При изучении движения ядер, напротив, следует учитывать не мгновенное положение электронов, а поле, создаваемое их средним пространственным распределением.

Таким образом суть адиабатического приближения состоит в том, что движение электронов и ядер можно считать независимым, происходящим без обмена энергией между электронной и ядерной подсистемами частиц.

Следствия:

а) Так как электронная и ядерная подсистемы независимы, то волновую функцию Y, как следует из теории вероятности, можно представить в виде произведения электронной Y_e и ядерной волновых функций:

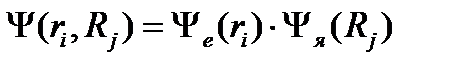(2.4)

б) Предположим, что ядра покоятся. Для этого случая кинетическая энергия ядер обращается в нуль.

в) Энергия взаимодействия электронов и ядер V_о принимает постоянное значение. Выбором начала отсчета энергии V _о можно обратить в нуль. Подстановка (2.4) в уравнение Шредингера (2.3) позволяет получить уравнение для электронов в кристалле в виде

(2.5)

где 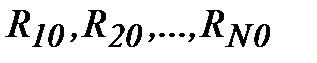— координаты покоящихся ядер, E, — соответственно энергия и волновая функция электронов.

2) Валентная аппроксимация.

Поскольку состояние внутренних атомных электронов мало изменяется в кристаллической решетке, то можно ограничиться рассмотрением только валентных электронов, а под 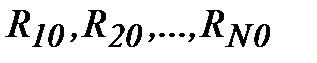подразумевать координаты не ядер, а атомных остатков. При этом уравнение (2.3) записывают только для валентных электронов, движущихся в потенциальном поле фиксированных атомных остатков.

Несмотря на проведенные упрощения, уравнение (2.3) не может быть решено в общем виде, так как по-прежнему имеем дело с многоэлектронной задачей. Чтобы свести многоэлектронную задачу к одноэлектронной, для этого сделаем ещё одно допущение.

Дата добавления: 2015-10-31