Плотность квантовых состояний.

Наиболее важной характеристикой электронного энергетического спектра является распределение электронных состояний по энергиям. Количественно описать это распределение можно, используя понятие " плотность состояний ".

Пусть в кристалле единичного объема в интервале энергий от Е до Е+dE имеется dZ квантовых состояний (безучета спина). В выбранном интервале энергии dE=const при различных значениях величины энергии Е число состояний dZ может различаться. Поэтому будем считать, что

во-первых, dZ зависит от величины Е, то есть dZ = dZ (Е);

во-вторых, связь между dZ и dE задается соотношением

, (2.1)

где коэффициент N, называемый плотностью состояний, также зависит от величины Е.

Физический смысл плотности состояний очевиден. Из соотношения (2.1) следует:

N(E) = , (2.2)

следовательно, плотность состояний – это число состояний в единичном интервале энергий для единичного объема кристалла.

Расчет величины N(Е) является довольно сложной квантовомеханической задачей, так как ее значениетесным образом связано с фор­мой изоэнергетических поверхностей. Действительно, построим в зоне Бриллюэна две изоэнергетические поверхности Е и Е+dE. Они выделяют некоторый слой в пространстве квазиимпульса (рис. 1). Пусть объем это­го слоя dt_p, ему соответствует объем фазо­вого пространства, то есть пространства координатx, y, z и импульсов p_x, p_y, p_z

(2.3)

Согласно принципа неопределенности Гейзенберга, минимальный объем фазовой ячейки, в которой может уместиться частица, равен h³_. . Следовательно, число фазовых ячеек в объеме фазового пространства dГ равно 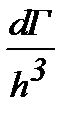, а число состояний для единичного объема

. (2.4)

Учитывая соотношения (2.1) и (2.3) следует

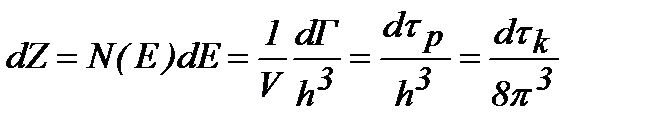(2.5)

Входящую в выражение (2.5) величину объема слоя в пространстве квазимпульса dt_k(E,E+dE) можно найти, если известно уравнение изоэнергетических поверхностей.

Рассмотрим некоторые частные случаи.

1. Предположим, что изоэнергетические поверхности имеют форму сферы с минимальной энергией E_min в центре зоны Бриллюэна. Пусть

(2.6)

Две изоэнергетические поверхности Е и Е+dЕ выделяют сферический слой толщиной dk и объемом dt_k(Е, Е+dE) (рис. 1):

(2.7)

Воспользовавшись соотношением (2.6), выразим k через E:

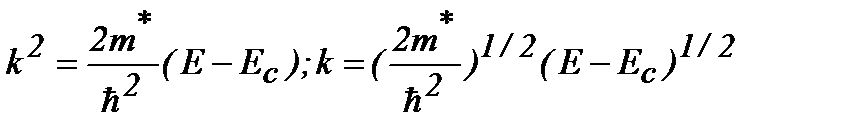(2.8)

Дифференцируя по k первое выражение в (2.9), получим

(2.9)

Учитывая соотношения (2.7), (2.8) и (2.9), можем записать

(2.10)

Для dZ из (2.5) и (2.10) получим

(2.11)

или

(2.12)

Таким образом, если энергия носителей заряда является квадратичной функцией квазимпульса, то плотность состояний N(Е) имеет зависимость от энергии вида .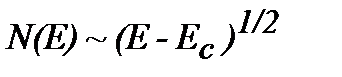

Дата добавления: 2015-10-31