Электронная теория примесных состояний.

Все реальные твёрдые тела содержат различные дефекты и примеси. Дефекты и примеси либо специально вводят в кристалл, либо они появляются на стадии выращивания.

Присутствие в определённом месте кристалла атома примеси или дефекта структуры приводит к тому, что на периодический потенциал решетки V(r) накладывается достаточно сильное возмущение V^*(r), локализованное в некоторой малой области с центром в точке r₀ (там, где расположен примесный атом или дефект).

Рассчитать положение уровней примесей или дефектов, даже если известен конкретный вид возмущения V^*(r), практически невозможно, т. к. неизвестен точный вид потенциала V(r). Однако пользуясь понятием эффективной массы, ур. Шредингера можно записать в виде

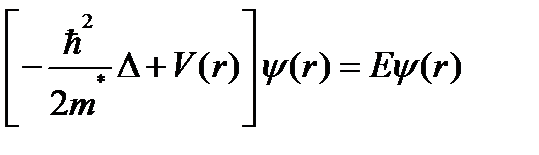(2.55)

Здесь уже отсутствует периодический потенциал, а появившаяся эффективная масса электрона может быть определена экспериментально. Данный метод решения уравнения Шредингера получил название метода эффективной массы.

Найдем в качестве примера положение локальных разрешенных уровней примесных атомов 5 группы таблицы Менделеева в элементарных полупроводниках 4 группы. Предположим, что в одном из узлов кристалла Ge находится атом мышьяка, имеющий пять электронов в валентной оболочке. Четыре валентных электрона участвуют в образовании связей ковалентных с четырьмя соседними атомами германия. Поскольку ковалентная связь является насыщенной, пятый электрон образовать новой связи не может. Находясь в кристалле, он сравнительно слабо взаимодействует с большим числом окружающих мышьяк атомов германия. Вследствие этого его связь с атомом As уменьшается и он движется по орбите большого радиуса. Его поведение подобно поведению электрона в атоме водорода.

Однако при этом необходимо учесть следующие обстоятельства:

1. электрон движется не только в кулоновском поле иона мышьяка, но и в периодическом поле решетки. Поэтому ему необходимо приписать эффективную массу m*.

3. взаимодействие электрона с атомным остатком, имеющим заряд Z_e,происходит в твердом теле, обладающим диэлектрической проницаемостью . С учетом этого потенциальная энергия электрона примесного атома

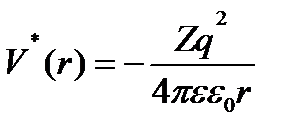(2.56)

2. расстояние между взаимодействующими зарядами достаточно велико, так что их можно считать точечными. Это будет иметь место, если орбита электрона примеси охватывает большое число узлов кристаллической решетки.

Учитывая все сказанное, УШ для пятого электрона мышьяка имеет вид:

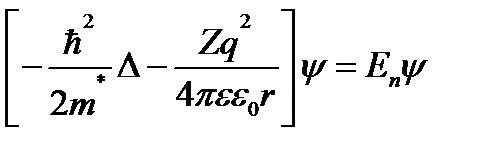(2.57)

По аналогии с решением уравнения Шредингера для атома водорода можно получить собственные значения энергии этого электрона

(2.58)

Здесь энергия отсчитывается от дна зоны проводимости (n- квантовое число).

Подставив численные значения e, m, h, 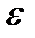₀ получим

(2.59)

где 13.52óвеличине в эВ энергии ионизации атома водорода.

Энергия ионизации примесного атома E_d равна по модулю энергии основного состояния (n=1)

(2.60)

Видно, что энергия ионизации атома примеси E_d в 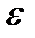² раз меньше энергии ионизации атома водорода.

Учитывая, что в Ge 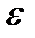=16, m*=0.25m получаем для энергии ионизации примесных атомов 5 группы E_d=0.01 эВ. В кремнии, где 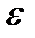=12

m*=0.4m-E_d=0.04 эВ

Т. о. достаточно весьма незначительной энергии чтобы перевести пятый электрон из связанного состояния в свободное, т.е. в зону проводимости. Примеси которые поставляют свободные электроны называются донорными.

Дефекты, способные отдавать электроны в зону проводимости называют донорами. Полупроводник, содержащий доноры называют полупроводник с электронной проводимостью или полупроводник n-типа.

Дефекты, способные принимать электроны из валентной зоны называют акцепторами. Полупроводник, содержащий акцепторы называют полупроводник с дырочной проводимостью или полупроводник p-типа.

Размеры области, в которой локализована волновая функция электрона, связанного с примесным атомом находится из соотношения

(2.61)

где а₀=0.53*10^-10м- радиус первой боровской орбиты атома водорода.

Для донорной примеси в Ge получаем а₁=64а₀=34*10^-10м. Т. к. постоянная решетки Ge равна 0.56 нм, отсюда следует, что эта орбита охватывает около 200 узлов решетки.

Радиус первой боровской орбиты примеси 5 группы в кремнии а₁=30а₀.

Т.о. использование кулоновского потенциала для вычисления энергии ионизации оправдано.

Предположим теперь, что один из узлов решетки германия замещен примесным атомом 3 группы таблицы Менделеева, например атом бора. Три валентных электрона атома бора образуют три ковалентных связи с соседними атомами германия, а четвертая связь остается незавершенной. Незавершенная связь есть ни что иное как дырка. Она ведет себя как частица с положительным зарядом. Атом бора может захватывать на незавершенную связь электрон основного вещества и превратиться в отрицательно заряженный ион. Дырка при этом становится свободной. Примеси, поставляющие свободные дырки, называются акцепторными. Собственные значения энергии для акцепторной примеси можно получить таким же путем, как они были получены для донорной примеси:

(2.62)

Здесь m*_p- эффективная масса дырки. Основной уровень акцепторной примеси (n=1), выраженный в эВ

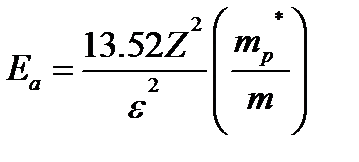(2.63)

должен находиться в запрещенной зоне выше потолка валентной зоны. Для Ge на 0.01эВ.

Дата добавления: 2015-10-31