Эффективная масса носителей заряда.

Как было показано при рассмотрении модели Кронига и Пенни, энергия электрона, движущегося в периодическом поле кристалла, E=p²/2m. Однако для практических целей удобно сохранить зависимость энергии электрона от квазиимпульса в классическом виде, а все различия, вызванные влиянием периодического поля, включить в массу электрона. Тогда в формуле Е р²/2m вместо т появляется некоторая функция энергии т*, называемая эффективной массой.

В одномерном случае величину т* можно рассчитать из разложения энергии в ряд Тейлора около экстремальных точек (т. к. E(k)- периодическая функция k и E(k)~cosk (периодический член))

(2.37)

Так как в точках k=k_o энергия имеет максимум или минимум (см. рис. 9), то первая производная равна нулю. Ограничиваясь вторым приближением, из (2.37) находим:

или

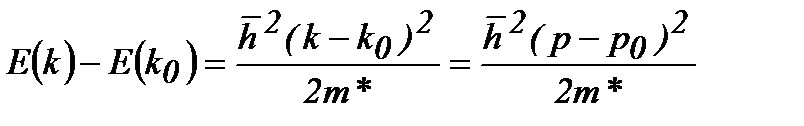
Следовательно, роль эффективной массы играет величина

В низших точках разрешенных зон Е(k) имеет минимумы, а вторая производная от Е по k больше нуля. Поэтому на дне зоны эффективная масса положительна, а в вершинах зон отрицательна, поскольку d²E/ dk²<0. В некоторой точке в центре зоны m* ® . Очевидно, разложение энергии в степенной ряд (2.43) и формула (2.44) справедливы только вблизи экстремальных точек. Понятие эффективной массы имеет более широкие границы применимости и может быть введено исходя из принципа соответствия.

Известно, что средние квантовомеханические величины удовлетворяют тем же соотношениям, что и соответствующие им классические величины. Так, волновые пакеты составленные из решений уравнения Шредингера, движутся по траекто­риям классических частиц. Поэтому уравнению Ньютона должен соответствовать квантовомеханический аналог, то есть квантовомеханическое уравнение движения электрона в кристалле. Найдем его. Для этого рассмотрим движение электрона под действием внешнего электрического поля.

Предположим сначала, что мы имеем дело со свободным электроном, помещенным в однородное электрическое поле . Со стороны поля на электрон будет действовать сила . Под действием этой силы он приобретает ускорение:

Здесь т — масса электрона. Вектор ускорения направлен так же, как вектор внешней силы, то есть против поля .

Теперь получим уравнение движения электрона, находящегося в периодическом поле кристалла. Внешнее поле действует на электрон в кристалле так же, как на свободный электрон, с силой , направленной против поля. В случае свободного электрона сила была единственной силой, определяющей характер движения частицы. На электрон же, находящийся в кристалле, кроме силы 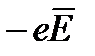действуют значительные внутренние силы, создаваемые периодическим полем решетки. Поэтому движение этого электрона будет более сложным, чем движение свободного электрона.

Движение электрона в кристалле можно описать с помощью волнового пакета, составленного из блоховских функций (7.22). Средняя скорость движения электрона равна групповой скорости волнового пакета:

. (2.38)

Учитывая, что для групповой скорости, получаем:

, (2.39)

где 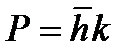-квазиимпульс. Видим, что средняя скорость элек­трона в твердом теле определяется законом дисперсии Е(). Продифференцируем (7.89) по времени:

^. (2.40)

За время электрическое поле совершит работу , которая идет на приращение энергии электрона :

. (2.41)

Учитывая, что

(2.42)

получаемиз (7.91)

, (2.43)

или

.(7.94) (2.44)

Последнее выражение представляет собой уравнение движения электрона в кристалле. В этом случае произведение равно силе F, действующей на электрон со стороны внешнего электрического поля. Для свободного электрона внешняя сила равна произведению . То, что для электрона в кристалле уравнение движения не имеет привычной формы второго закона Ньютона, не означает, что закон Ньютона здесь не выполняется. Все дело в том, что уравнение движения мы записали только с учетом внешних сил, действующих на электрон, и не учли силы, действующие со стороны периодического поля кристалла. Поэтому не удивительно, что уравнение движения не имеет обычного вида

Подставим теперь 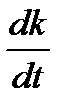найденноеиз (2.44), в выражениедля ускорения (2.40):

Уравнение (7.95) связывает ускорение электрона a с внешней силой - еЕ. Если предположить, что величина имеет смысл массы, то (7.95) приобретает вид второго закона Ньютона:

(2.45)

где

(2.46)

Величина т* получила название эффективной массы электрона. Эффективная масса отражает влияние периодического потенциала решетки на движение электрона в кристалле под действием внешней силы. Из (7.96) следует, что электрон в периодическом поле кристаллической решетки движется под действием внешней силы F в среднем так, как двигался бы свободный электрон под действием этой силы, если бы он обладал массой т* Таким образом, если электрону в кристалле вместо массы т приписать эффективную массу т*, то его можно считать свободным и движение этого электрона описывать так, как описывается движение свободного электрона, помещенного вовнешнее поле. Разница между т* и m обусловлена взаимодействием электрона с периодическим полем решетки, и, приписывая электрону эффективную массу, мы учитываем это взаимодействие.

Эффективная масса, в отличие от обычной массы, не определяет ни инерционных, ни гравитационных свойств частицы. Она является лишь коэффициентом в уравнении движения (7.95) и отражает меру взаимодействия электрона с кристаллической решеткой.

Пользуясь понятием эффективной массы, задачу о движении электрона в периодическом поле решетки V() можно свести к задаче о движении свободного электрона с массой т*. Это значит, что вместо уравнения Шредингера с периодическим потенциалом

нужно решать уравнение

.

Если, например, энергия является квадратичной функцией от| к, то ее можно записать так, как это было сделано в (7.36) для свободного электрона:

(2.47)

Легко видеть, что для свободного электрона эффективная масса равна его обычной массе. В этом случае связь между Е и k дается соотношением (7.36), откуда получаем

и . (2.48)

В общем случае эффективная масса является анизотропной величиной и для разных направлений волнового вектора различна. Она представляет собой тензор второго ранга:

или

Таким образом, если зависимость [закон дисперсии ] анизотропная, то эффективная масса представляет собой тензор (тензор обратных эффективных масс):

Это означает, что ускорение электрона в решетке в общем случае направлено не параллельно внешней силе . Оно может быть направлено даже антипараллельно , что соответствует отрицательному значению

Отрицательная эффективная масса означает, что ускорение электрона направлено против действия внешней силы. Это видно из рис. 7.15 б. При k, близких к границе зоны Бриллюэна, несмотря на увеличение к, скорость электрона уменьшается. Данный результат является следствием брэгговского отражения. В точке k= — электрон описывается уже не бегущей,а стоячей волной и =0.

Поскольку свойства электронов с отрицательной эффективной массой очень сильно отличаются от свойств "нормальных" электронов, их удобнее описывать, пользуясь представлением о некоторых квазичастицах, имеющих заряд +е, но положительную эффективную массу. Такая, квазичастица получила название дырка.

(Почему используется термин “квазичастица”? Дырка существует лишь, то время, когда она не рекомбинировала с электроном. Электрон существует всегда: , (дырка появляется и исчезает с квантом энергии, следовательно, квазичастица)).

Предположим, что в зоне все состояния, кроме одного, заняты электронами. Вакантное состояние вблизи потолка зоны и называют дыркой. Если внешнее поле равно нулю дырка занимает самое верхнее состояние. Под действием поля на это вакантное состояние перейдет электрон с более низкого энергетического уровня. Дырка при этом опустится. Далее дырочное состояние займет следующий электрон и т. д. При этом дырка будет смещаться вниз по шкале энергий. Таким образом, ток в кристаллах может переноситься не только электронами в зоне проводимости, но и дырками в валентной зоне. Дырочная проводимость наиболее характерна для полупроводников, однако есть и некоторые металлы, которые обладают дырочной проводимостью.

Возвращаясь к рис. 7.15 в, отметим, что описывать движение электронов в кристалле, пользуясь понятием эффективной массы, можно только тогда, когда они находятся либо у дна, либо у потолка энергетической зоны. В центре зоны m* теряет смысл. На практике почти всегда приходится иметь дело с| электронами, располагающимися или у дна, или у потолка зоны. Поэтому использование эффективной массы в этих случаях вполне оправдано.

Ширина зон растет с увеличением числа. Следовательно, зона проводимости как правило имеет большую ширину, чем валентная зона.

Поскольку эффективная масса обратно пропорциональна ширине энергетической зоны, следовательно .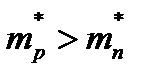

Следовательно, дырка и электрон проводимости отличаются не только знаком своего заряда, но имеют и разные величины m*.

Как отмечалось выше, каждому положительному направлению волнового вектора k разрешенной зоне соответствует состояние с волновым вектором, равным — k. Поэто­му если все состояния заняты, то всякое перемещение одного электрона компенсируется противоположным перемещением другого электрона. И несмотря на возможно большую ско­рость электронов, ток в полупроводнике отсутствует, даже если к нему приложено внешнее электрическое поле.

Иной результат получается, если в почти заполненной зоне имеются свободные места, то есть не все валентные связи обеспе­чены электронами. Тогда соседние электроны могут переходить на эти места, а само свободное место как бы перемеща­ется в пространстве. В энергетическом плане это соответству­ет переходу электронов с низких энергетических уровней на более высокие, а дырок с высоких уровней на более низкие.

Вместо того чтобы рассматривать движение всей совокупности электронов почти заполненной зоны, более удобно и просто следить за движением вакантных мест, называемых дырками. В этом случае плотность тока равна

где суммирование проводится по всем значениям волнового вектора в первой зоне Бриллюэна k и двум состояниям спина электрона 1,2. Символ 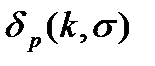равен единице, если состояние свободно, и нулю, если оно занято;

n (k) — скорость электрона;

V— объем кристалла. Сумма равна нулю, поскольку она берется по всем состояниям зоны.

Ток частично заполненной зоны может быть представлен как ток положительно заряженных частиц дырок. Заряд дырки положителен и равен по величине заряду электрона. Концентрация дырок обычно обозначается буквой р. Понятие дырок применимо при рассмотрении всех физических процессов в полупроводниках. Эффективная масса дырки m * равна эффективной массе электрона, взятой с обратным знаком. У потолка валентной зоны эффективная масса электрона отрицательна, а m *>0.

Таким образом, суммируем полученную информацию:

1. Обозначения носителей зарядов в полупроводнике.

Электроны	n, e (electrons negative)
Дырки	p, h (holes positive)

2. Представления о дырках:

Три представления (определения) дырок:

1) полнокровная положительно заряженная частица, перемещающая в кристалле.

2) отсутствие электрона в потолке валентной зоны.

3) физическое отсутствие электрона в том месте, где он должен быть в равновесном состоянии.

3. Направление энергии в зонах:

Проводимости растет

Валентная убывает

4. Величина m * зависит от кривизны зоны

5.Ширина зон растет с увеличением E (из уравнения Кроника-Пени), следовательно зона проводимости энергетически шири, чем валентная; т.к. m^* обратно пропорциональна ширине энергетической зоны, следовательно (как правило) значит дырка и электрон отличаются не только знаком заряда, но и величиной эффективной массы.

---

Дата добавления: 2015-10-31