
Читайте также:
|
Его суть заключается в том, что энергию попарного взаимодействия электронов заменяют энергией взаимодействия каждого электрона с усредненным полем всех остальных электронов. Это поле получило название самосогласованного, так как оно не только определяет движение данного электрона, но и само зависит от его движения. Введение самосогласованного поля позволяет рассматривать электроны в кристалле как невзаимодействующие частицы, т.е. движущиеся не зависимо друг от друга. Это и является основанием для представления электронов проводимости в виде идеального газа и в уравнении (2.3) двойную сумму  заменить суммой
заменить суммой 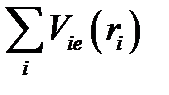 а
а  -суммой
-суммой 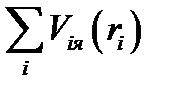 ,
,
где  — потенциальная энергия i-го электрона в поле всех остальных электронов,
— потенциальная энергия i-го электрона в поле всех остальных электронов,  — потенциальная энергия i-го электрона в поле всех ядер.
— потенциальная энергия i-го электрона в поле всех ядер.
После такой замены уравнение (2.3) распадается на сумму п одинаковых для всех электронов индивидуальных одноэлектронных уравнений вида
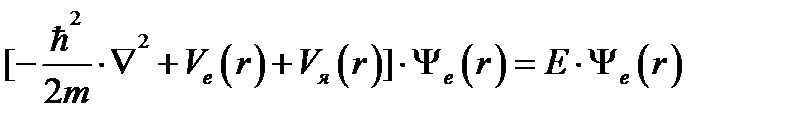 , (2.6)
, (2.6)
где  и Е— соответственно волновая функция и энергия электрона в кристалле.
и Е— соответственно волновая функция и энергия электрона в кристалле.
Обозначив потенциальную энергию электрона в кристалле через функцию  равную
равную
 (2.7)
(2.7)
уравнение (24) можно записать так:
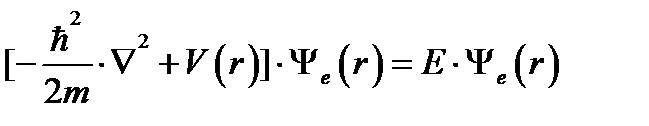 (2.8)
(2.8)
Таким образом, в результате обоих приближений удалось свести задачу к обычному по форме уравнению Шредингера, но с другой функцией. В изолированном атоме, как известно, потенциальная фунция имеет вид гиперболы (см. рис. 13). В кристалле, соответственно, будет чередующийся ход таких гипербол, схематично изображенный на рис. 14.
Существуют различные способы радиального выбора вида функции V(r) для решения одноэлектронной задачи. Наиболее часто для этого используются состояние электрона, находящегося в потенциальном поле всех ионов решетки, заряд которых в среднем скомпенсирован зарядом валентных электронов, т. е. в поле периодического потенциала. Другими словами: член V(r) есть полный потенциал кристалла, обладающий трехмерной периодичностью решетки.
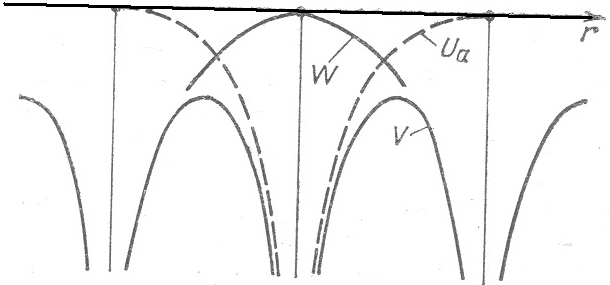
Рис.2.Схематическое изображение периодического потенциала одномерной решётки.
Сплошная кривая – потенциал решётки  ;пунктирная – атомный потенциал
;пунктирная – атомный потенциал 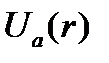 ;штрихпунктирная – возмущающий потенциал
;штрихпунктирная – возмущающий потенциал  .
.
Так как в кристалле атомы расположены строго периодически, то полный потенциал кристалла V(r) должен обладать трехмерной периодичностью. Точный вид периодического потенциала V(r) неизвестен. Однако тот факт, что V(r) является периодической функцией, период которой совпадает с периодом кристаллической решетки, то есть:
V(r) = V(r+g) (2.9)
где g – вектор трансляции, позволяет получить два фундаментальных результата.
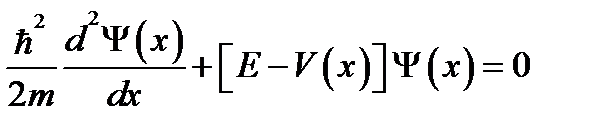
Первый. Из условия трансляционной симметрии следует, что волновая функция электрона в точке r отличается от волновой функции электрона в точке r+g некоторым множителем С.
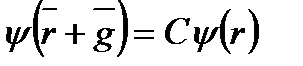 (2.10)
(2.10)
Из условия нормировки следует, что
 (2.11)
(2.11)
Условию (29) можно удовлетворить, если положить
С = exp(ikg) (2.12)
Заметим, что вектор трансляции имеет размерность длины. Следовательно, волновой вектор k должен иметь размерность, обратную длине, то есть см-1.
На основании соотношений (2.11) и (2.9), можно показать, что волновая функция электрона в кристалле имеет вид:
 , (2.13)
, (2.13)
где  — периодическая функция,
— периодическая функция,  — плоская волна, идущая в направлении вектора k.
— плоская волна, идущая в направлении вектора k.

 можно полагать, что
можно полагать, что 
т. к. 
Здесь k-постоянный вектор, характеризующий квантовое состояние электрона в кристалле, называется волновым вектором.
kg- безразмерное, следовательно  и
и 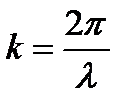


Где  функция
функция 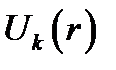 обладает трех мерной периодичностью кристаллической решетки т. к.
обладает трех мерной периодичностью кристаллической решетки т. к.
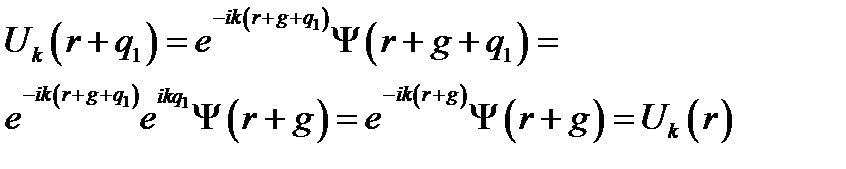

Таким образом: стационарная волновая функция электронов в периодическом поле кристалла зависит от волнового вектора  и имеет вид
и имеет вид  , где
, где  — плоская волна, бегущая в направлении
— плоская волна, бегущая в направлении  , а функция координат
, а функция координат  - функция координат, зависящая от волнового вектора
- функция координат, зависящая от волнового вектора  и имеющая периодичность решетки.
и имеющая периодичность решетки.
 - носит название волны или функции Блоха
- носит название волны или функции Блоха
Волны, описываемые соотношением (2.13), носят название волн Блоха. Волна Блоха представляет собой плоскую волну, модулированную периодической функцией  , имеющей период решетки и зависящий от волнового вектора k. Волновой вектор k задает направление распространение плоской волны. Физический смысл волнового вектора k – число длин волн, укладывающихся на отрезке 2p.
, имеющей период решетки и зависящий от волнового вектора k. Волновой вектор k задает направление распространение плоской волны. Физический смысл волнового вектора k – число длин волн, укладывающихся на отрезке 2p.
Второй результат является следствием неоднозначности волнового вектора k для электрона в кристалле. Чтобы показать это, рассмотрим трансляционное условие:
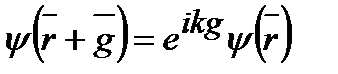 (2.14)
(2.14)
Это условие не нарушится, если волновой вектор k заменить на вектор k +2p К, где
 . (2.15)
. (2.15)
Вектор К называют вектором обратной решетки.
Следовательно, состояния, характеризуемые волновым вектором k и k + 2pК физически эквивалентны. То есть энергия электронов, находящихся в этих двух= состояниях одинакова. Другими словами, и волновая функция и энергия электрона в кристалле являются периодическими функциями волнового вектора k с периодом 2pК:
 (2.16)
(2.16)
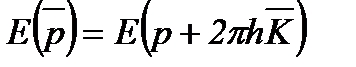 (2.17)
(2.17)
Если в k -пространстве (или в P-пространстве) построить обратную решетку, растянутую в 2p раз, то есть решетку с векторами 2pb1, 2pb2, 2pb3 (или  ,
, 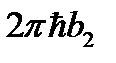 ,
, 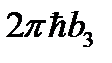 ) то все k -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.
) то все k -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.
Многогранник минимального объема, построенный вокруг начала координат в k-пространстве, содержащей все возможные различные состояния, называют первой или основной зоной Бриллюэна. С помощью векторов обратной решетки любую точку k -пространства можно перевести в первую зону Бриллюэна.

Рис.3
Дата добавления: 2015-10-31; просмотров: 390 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Адиабатическое приближение (приближение Борна - Оппенгеймера). | | | Первая зона Бриллюэна полупроводника типа алмаза |