Корпускулярно – волновой дуализм. Соотношение неопределенностей Гейзенберга.

Лекция 4

4.1. Гипотеза де Бройля. Волны де Бройля.

По представлениям классической физики движение частиц и распространение волн – принципиально разные физические процессы. Однако фотоэффект и эффект Комптона убедительно показали, что свет – объект, имеющий согласно классической теории, волновую природу, обнаруживает сходство с потоком частиц – фотонов, обладающих энергией и импульсом, которые связаны с частотой и длиной волны света соотношениями

, . (4.1)

В 1924 году Луи де Бройль выдвинул гипотезу, согласно которой дуализм присущ не только фотонам, но и вообще всем микрообъектам. Толчком к осознанию этого удивительного факта послужило следующее соображение. Де Бройль пытался выяснить, чем выделены стационарные орбиты в теории Бора. Он заметил, что в длину окружности стационарной орбиты укладывается целое число длин волн, определенных равенством (4.1)

. (4.2)

Де Бройль посчитал, что это не случайно и высказал предположение, что с движущимся электроном связан некоторый волновой процесс. Связь между волновыми и корпускулярными характеристиками электрона описывается той же формулой, что и для фотона.

. (4.3)

Эти волны получили название волн де Бройля.

Для экспериментального подтверждения этой гипотезы нужно было получить дифракцию электронов на каком либо дифракционном устройстве. Сложность такого эксперимента заключалась в том, что длина волны де Бройля достаточно мала. Из соотношения (4.2) видно, что 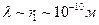. Для наблюдения дифракции нужно выполнение условия , где – постоянная решетки. Ясно, что сделать решетку с такой малой постоянной не представляется возможным. Однако в природе есть естественные решетки с постоянной, сравнимой с длиной волны де Бройля – это кристаллы. В них ионы расположены на равных расстояниях друг от друга, образуя затемненные участки этой своеобразной дифракционной решетки. Наиболее четкой дифракционная картина получается при использовании

монохроматического света. Для создания монохроматического пучка электроны пропускают через ускоряющую разность потенциалов, в результате чего они приобретают одинаковую скорость и, следовательно, будут иметь одинаковую длину волны

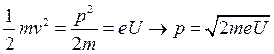, (4.4)

. (4.5)

После прохождения электронами тонкой металлической фольги на экране наблюдалась дифракционная картина, ничем не отличающаяся от дифракционной картины для световых волн (Рис. 4.1). Максимумы интенсивности располагались под углами, определенными уравнением решетки .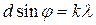

Рис. 4.1

Таким образом, понятие корпускулярно – волнового дуализма было распространено на все микрообъекты. Для частиц с большой массой длина волны де Бройля оказывается слишком малой для того, чтобы ее можно было определить экспериментально. В этом случае волновые свойства частицы не проявляются.

4.2. Соотношение неопределенностей Гейзенберга

Успех теории Бора был достигнут за счет нарушения логической цельности теории: с одной стороны использовалась классическая механика, с другой – привлекались чуждые ей правила квантования, к тому же противоречащие классической электродинамике. Теория Бора не могла ответить на вопрос, как движется электрон при переходе с одного уровня на другой во время квантового скачка. Конечная скорость движения, требуемая теорией относительности, означала, что энергия электрона не может измениться сразу на величину поглощенного кванта. Совершенной загадкой также оставался вопрос о том, откуда электрон знает какой квант ему нужно поглотить, чтобы оказаться точно на одном из возбужденных уровней. Не меньшие трудности представляла и проблема интерференции микрочастиц. Хотя электрон является неделимым и, следовательно, может проходить лишь через одно из отверстий, но наличие альтернативного пути каким то образом влияет на распределение вероятностей попадания электрона в различные точки экрана. Все эти противоречия ясно указывали на то, что в микромире классические представления не применимы.

Важным шагом на пути становления новой квантовой теории явился установленный Гейзенбергом принцип неопределенностей, который является основополагающим принципом квантовой механики. Он гласит: не существует такого состояния, в котором координата и импульс частицы имеют определенные точные значения.

Пусть 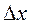– неопределенность координаты частицы, а 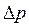– неопределенность ее импульса, тогда математически принцип неопределенностей может быть сформулирован так:

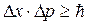. (4.6)

Это формула называется соотношением неопределенностей Гейзенберга. Из нее следует, что чем точнее мы знаем одну из переменных, например, координату, тем менее определенной становится другая. Действительно, если координата известна, это означает, что 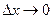. Тогда 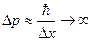, то есть импульс частицы становится полностью неопределенным. Отметим, что неопределенности координаты и импульса никак не связаны с погрешностями определения этих величин на опыте. Никакой эксперимент не может привести к одновременному, точному измерению координаты и импульса частицы. Это, в частности, означает, что понятие траектории не применимо к движению микрообъекта.

Такое же соотношение существует и для другой пары величин

. (4.7)

Это соотношение означает, что для определения энергии с точностью нужно затратить время не меньшее, чем .

Соотношение неопределенностей является следствием двух положений:

1. Оно показывает границы применимости макро понятий к микрообъекту. В макромире были выработаны два взаимоисключающие понятия – волны и частицы. При применении их к микрообъектам оказалось, что они подходят для их описания лишь приблизительно. Микрообъект не является ни волной, ни частицей. Он способен проявлять то или иное свойство в зависимости от условий эксперимента. Соотношение неопределенностей и выражает меру применимости макро понятий к микрообъекту.

2. В микромире измерение есть всегда процесс взаимодействия микрообъекта с классическим прибором. В макромире воздействие измерительного прибора на измеряемый объект всегда можно сделать сколь угодно малым, то есть измерение не изменяет состояние исследуемого объекта. В микромире воздействие измерительного прибора может существенно изменить состояние микрообъекта. Энергию взаимодействия между прибором и исследуемой системой можно учесть лишь с точностью .

Насколько существенно воздействие прибора на измеряемый объект продемонстрируем на следующем примере. Пусть электроны, вылетающие из источника, проходят через диафрагму с двумя отверстиями и попадают на экран (Рис. 4.2). Если закрыть одно из отверстий, то вероятность обнаружить электрон в определенной точке экрана, будет равна 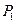, если закрыть второе отверстие, то вероятность будет (Рис. 4.2, а). Если же оба отверстия открыть, то полная вероятность обнаружить электрон в какой то точке экрана не будет равна сумме вероятностей (Рис. 4.2, б).

На экране будет наблюдаться интерференционная картина. Таким образом, наличие двух возможных путей перехода электрона от источника к экрану существенным образом влияет на распределение вероятностей, и поэтому нельзя сказать каким путем прошел электрон. Приходится считать, что он одновременно мог пройти двумя различными путями. Возникающие представления, действительно, радикально отличаются от классических: невозможно представить себе движение частицы одновременно по двум траекториям.

Давайте изменим опыт так, чтобы можно было определить по какому пути электрон прошел от источника к экрану. Например, поставим за каждым из отверстий источник фотонов. При рассеянии электрона на фотоне мы будем наблюдать вспышку света за одним из отверстий. Мы увидим, что электрон, действительно, всегда проходит либо через первое отверстие, либо через второе. Но, посмотрев на экран, увидим, что интерференционная картина исчезла и , как и должно быть для частиц. В первом опыте, электроны ведут себя как классические волны. Во втором опыте измерение выделяет одну из траекторий, делая другие невозможными, и электроны ведут себя как классические частицы.

Из этого примера видно, что измерительный прибор сам участвует в формировании изучаемого на опыте явления и эту его роль нельзя не учитывать. Мы не можем одновременно измерить координату и импульс частицы потому что, производя измерение одной величины, мы вносим неустранимые возмущения в ее движение и искажаем значение другой величины. Роль измерительного прибора особо подчеркивалась создателями квантовой механики Бором и Гейзенбергом. Вопрос, по какой траектории двигался электрон в интерференционном опыте, Гейзенберг считал бессмысленным, так как, либо нет траектории, либо нет интерференции. Он особо подчеркивал, что имеет смысл ставить только такие вопросы, ответ на которые можно получить из эксперимента.

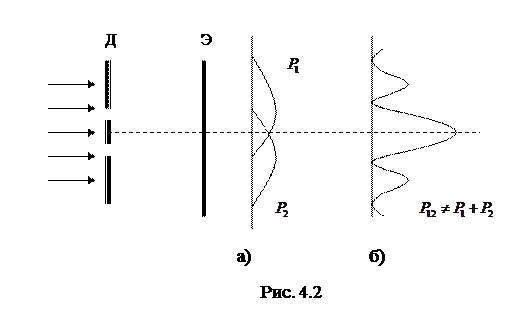
Из приведенных выше рассуждений может сложиться впечатление, что на самом деле частица имеет определенное значение координаты и импульса, просто мы не можем их измерить на опыте одновременно и точно. На таком выводе настаивал Эйнштейн, относя ограничения, вводимые соотношением неопределенностей, на счет несовершенства теории. Эйнштейн, Подольский и Розен придумали мысленный эксперимент, который на первый взгляд противоречил принципиальному запрету одновременного определения координаты и импульса частицы. Допустим, две частицы А и В образовались в результате распада третьей частицы С. В этом случае по закону сохранения импульса их суммарный импульс должен быть равен импульсу исходной частицы . Это дает нам возможность измерить импульс одной частицы, например, А и рассчитать значение импульса второй частицы 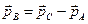, не внося в ее движение никаких возмущений. Поэтому, измерив

координату частицы В, мы сумеем получить для этой частицы значение двух не измеряемых одновременно величин. Таким образом, получается, что соотношение неопределенностей не является абсолютным, а законы квантовой механики неполны и должны быть уточнены. Это – знаменитый парадокс Эйнштейна, Розова, Подольского. Несмотря на кажущуюся убедительность этих рассуждений, они не верны. Дело в том, что в их основе лежат классические представления о движении частиц. Согласно квантовой механике, две частицы, образующиеся при распаде третьей, всегда остаются связанными между собой. Возмущение, вносимое измерением в состояние первой частицы, мгновенно возмущает состояние второй, после чего искажается значение второй физической величины, как у первой частицы, так и у второй. Связанные таким образом частицы называются в квантовой механике запутанными. Как мы увидим в дальнейшем, запутанные частицы описываются единой волновой функцией, на каком бы расстоянии друг от друга они не находились.

В настоящее время нет сомнений в том, что микрообъекты не обладают одновременно определенными значениями координат и импульсов. Из соотношения неопределенностей вытекает, что локализованный электрон должен иметь больший импульс. Если электрон локализован в области, размером , тогда

и 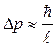. (4.8)

Чем меньше размер области локализации, тем больше будет неопределенность импульса и, следовательно, средний импульс 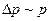. А это, в свою очередь, означает, что возрастает кинетическая энергия электрона

. (4.9)

Поэтому для локализации электрона нужна энергия. Если ничто не препятствует движению электрона, то неопределенность импульса стремится разрушить с течением времени первоначальную локализацию частицы. Однако если электрон локализовать внешними силами, например, поместив его в потенциальную яму, то он будет оказывать давление на стенки ямы. Чем в меньшей области локализован электрон, тем большая нужна энергия, чтоб его в этой области удерживать. Невозможно заставить электрон занять вполне определенное положение и оставаться там в покое.

Интересно отметить, что формула (4.9) позволяет оценивать энергию связи частицы, зная размеры области ее локализации. Например, для электрона, локализованного в пределах первой Боровской орбиты (), получаем

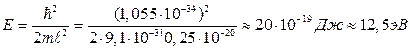. (4.10)

Это значение энергии довольно точно совпадает с энергией электрона в основном состоянии атома водорода, полученной в теории Бора.

Для протона, локализованного в пределах ядерных размеров (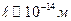), получаем

. (4.11)

Как мы увидим дальше, энергия связи протонов в ядре, действительно, такого порядка величины. Отметим, что для локализации электрона в пределах ядра была бы необходима энергия в 2000 раз большая, чем для локализации протона. Отсюда сразу же следуют два важных вывода. Во-первых, электроны не могут входить в состав ядра. Во-вторых, электрон не может упасть на ядро, поскольку в атоме нет сил, способных его там удержать. При такой локализации он будет иметь столь большую энергию, что неизбежно покинет пределы атома.

Соотношение неопределенностей позволяет обойти трудности, о которых мы упоминали в начале лекции. Оно делает бессмысленным вопрос о том, как происходит квантовый скачок. Неопределенность энергии электрона во время перехода с одного уровня на другой так велика, что никакие детали ее изменения не поддаются экспериментальному определению, и, следовательно, обсуждать их бессмысленно. Да и само понятие квантового скачка не следует понимать буквально. Теперь нам понятно, что электрон внутри атома не движется по каким либо стационарным орбитам, ведь на них определенное значение имеют и координата, и импульс частицы, а это невозможно. Мы можем лишь утверждать, что электрон размазан по области порядка размера атома, но имеет более или менее определенное значение энергии. При взаимодействии электрона с фотоном происходит более сильная локализация электрона в пространстве координат, но расплывание его состояния в пространстве энергий, так что эта область делокализации покрывает все возможные значения энергий электрона в атоме. После поглощения кванта света начинается обратный процесс. Электрон расплывается в координатном пространстве, то есть делокализуется по всему размеру атома, но локализуется в пространстве энергий, приобретая новое значение энергии, которое соответствует одному из возбужденных состояний. Причем мы можем предсказать лишь вероятность того, на каком возбужденном уровне электрон окажется. Точный результат взаимодействия электрона с фотоном установить невозможно.

Дата добавления: 2015-10-30