
Движение носителей заряда в образце полупроводника может возникать прежде всего под действием электрического поля или разности потенциалов. Образующийся электрический ток называют дрейфовым. Кроме того, движение носителей может обуславливаться пространственной неоднородностью их концентрации. При этом возникает так называемый диффузный ток.
Сначала более детально остановимся на механизме дрейфовой электропроводности.
Электропроводность полупроводника, как и всех твердых тел, определяется характером зонного энергетического спектра для электронов и конкретным характером распределения их по уровням энергии.
У полупроводника, в отличие от металлов, проводящее состояние является возбуждённым, поскольку для обеспечения их проводимости необходимо наличие электронов в зоне проводимости или свободных дырок в валентной зоне. Но для создания носителей тока обоих типов необходимо затратить энергию, необходимую для перевода электронов в зону проводимости или на локальные акцепторные уровни из валентной зоны, вследствие чего в последней появляются свободные дырки. В нормальном невозбуждённом состоянии при  полупроводник, не имея ни электронов проводимости, ни дырок в валентной зоне, тока не проводят.
полупроводник, не имея ни электронов проводимости, ни дырок в валентной зоне, тока не проводят.
Под действием сил приложенного электрического поля 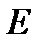 носители тока в полупроводнике приобретают в направлении действующих сил составляющие скоростей, налагающееся на их хаотическое тепловое движение. В результате этого нарушается симметрия их распределения по импульсам.
носители тока в полупроводнике приобретают в направлении действующих сил составляющие скоростей, налагающееся на их хаотическое тепловое движение. В результате этого нарушается симметрия их распределения по импульсам.
Носители тока в полупроводнике движутся не свободно, а под действием сил периодического поля кристаллической решетки.но, как было показано ранее, если электронам или дыркам приписать эффективную массу  , то их можно считать свободными частицами, движущимися под действием тех или иных внешних сил. Поэтому уравнения движения для носителей тока в кристалле будут такими же, как и соответствующие уравнения для свободных частиц.
, то их можно считать свободными частицами, движущимися под действием тех или иных внешних сил. Поэтому уравнения движения для носителей тока в кристалле будут такими же, как и соответствующие уравнения для свободных частиц.
Как известно, под действием электрического поля напряженностью  электроны получают ускорение
электроны получают ускорение  и направленную по полю добавку к скорости
и направленную по полю добавку к скорости  , где
, где  - время, в течении которого действует ускорение
- время, в течении которого действует ускорение  . Если бы
. Если бы  не было ничем ограничено, то и скорость электрона в направлении поля неограниченно возрастала бы. В действительности это не так. В идеальном кристалле с покоящимися атомами, характеризующемся периодичностью поля кристаллической решетки, электроны действительно должны двигаться ускоренно на протяжении очень больших промежутков времени. Но идеальных кристаллов не существует. В реальных кристаллах всегда существуют нарушения периодичности потенциала решетки, обусловленные, во первых тепловыми колебаниями атомов, и во вторых, всевозможными дефектами решетки.
не было ничем ограничено, то и скорость электрона в направлении поля неограниченно возрастала бы. В действительности это не так. В идеальном кристалле с покоящимися атомами, характеризующемся периодичностью поля кристаллической решетки, электроны действительно должны двигаться ускоренно на протяжении очень больших промежутков времени. Но идеальных кристаллов не существует. В реальных кристаллах всегда существуют нарушения периодичности потенциала решетки, обусловленные, во первых тепловыми колебаниями атомов, и во вторых, всевозможными дефектами решетки.
В силу этого электрон лишь на сравнительно небольшом отрезке пути  движется ускоренно, затем испытывает соударение, теряет при этом свою направленную скорость, и весь процесс начинается сначала. Среднее расстояние между двумя последовательными столкновениями называются длиной свободного пробега частицы. Оно составляет
движется ускоренно, затем испытывает соударение, теряет при этом свою направленную скорость, и весь процесс начинается сначала. Среднее расстояние между двумя последовательными столкновениями называются длиной свободного пробега частицы. Оно составляет  . Так как средняя скорость электрона порядка
. Так как средняя скорость электрона порядка  , то время свободного пробега
, то время свободного пробега  оказывается порядка
оказывается порядка  . При высоких температурах длину свободного пробега ограничивают тепловые колебания атомов, при низких – примеси и другие дефекты кристаллов.
. При высоких температурах длину свободного пробега ограничивают тепловые колебания атомов, при низких – примеси и другие дефекты кристаллов.
Средняя скорость, с которой электрон будет двигаться вдоль поля
 (3.1.1)
(3.1.1)
где  - отношение скорости дрейфа электронов к электрическому полю.
- отношение скорости дрейфа электронов к электрическому полю.
*) здесь  = тепловой скорости электронов. Это справедливо при движении электрона в не очень сильных полях, (т.е. когда
= тепловой скорости электронов. Это справедливо при движении электрона в не очень сильных полях, (т.е. когда  ):
):  .
.
При комнатной температуре  , полагая тепловую скорость
, полагая тепловую скорость  и
и  , получим
, получим  . В этом случае критическое поле
. В этом случае критическое поле  .
.

Величина  - называется подвижностью. Подвижность – это скорость дрейфа электронов в поле напряженностью
- называется подвижностью. Подвижность – это скорость дрейфа электронов в поле напряженностью  .
.
Более строгий расчет даёт в 2-раза большее значение подвижности:
 (3.1.2)
(3.1.2)
Если  содержит
содержит  свободных электронов и все они движутся в направлении поля со скоростью
свободных электронов и все они движутся в направлении поля со скоростью  , то через площадку в
, то через площадку в  за секунду пройдут все электроны, находящиеся в объёме параллелепипеда длиной
за секунду пройдут все электроны, находящиеся в объёме параллелепипеда длиной  . Число таких электронов будет
. Число таких электронов будет  . Заряд, переносимый этими электронами называется плотностью тока:
. Заряд, переносимый этими электронами называется плотностью тока:
 (3.1.3)
(3.1.3)
Следовательно, удельная объемная проводимость, вызванная движением электронов,
 (3.1.4)
(3.1.4)
Аналогичной формулой описывается дрейфовое движение дырок:
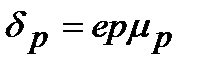 (3.1.5)
(3.1.5)
 - подвижность дырок,
- подвижность дырок,  .
.
Электрическое поле напряженностью  действует как на электроны, так и на дырки. Так как знаки зарядов и скорости этих частиц противоположны, то соответствующие токи складываются. Поэтому в области собственной и смешанной проводимости:
действует как на электроны, так и на дырки. Так как знаки зарядов и скорости этих частиц противоположны, то соответствующие токи складываются. Поэтому в области собственной и смешанной проводимости:
 (3.1.6)
(3.1.6)
где
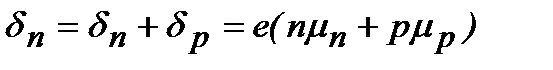 - удельная объемная проводимость материала.
- удельная объемная проводимость материала.
При наличии нескольких сортов носителей заряда с различными массами и подвижностями:
 (3.1.7)
(3.1.7)
где суммирование проводиться по всем сортам носителей.
Дрейфовый ток, обусловленный не основными носителями пренебрежимо мал по сравнению с током, который связан с основными носителями.
Еще раз заостряю внимание на следующем: в полупроводнике  - типа вектор напряженности поля и скорости электронов направлены в разные стороны, а в
- типа вектор напряженности поля и скорости электронов направлены в разные стороны, а в  - типе – одинаково направлены, т.е.
- типе – одинаково направлены, т.е.
Подвижность
Величина  - называется подвижностью. Подвижность – это скорость дрейфа электронов в поле напряженностью
- называется подвижностью. Подвижность – это скорость дрейфа электронов в поле напряженностью  .
.
Более строгий расчет даёт в 2-раза большее значение подвижности:
 (3.1.2)
(3.1.2)
Если  содержит
содержит  свободных электронов и все они движутся в направлении поля со скоростью
свободных электронов и все они движутся в направлении поля со скоростью  , то через площадку в
, то через площадку в  за секунду пройдут все электроны, находящиеся в объёме параллелепипеда длиной
за секунду пройдут все электроны, находящиеся в объёме параллелепипеда длиной  . Число таких электронов будет
. Число таких электронов будет  . Заряд, переносимый этими электронами называется плотностью тока:
. Заряд, переносимый этими электронами называется плотностью тока:
 (3.1.3)
(3.1.3)
Следовательно, удельная объемная проводимость, вызванная движением электронов,
 (3.1.4)
(3.1.4)
Аналогичной формулой описывается дрейфовое движение дырок:
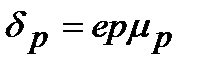 (3.1.5)
(3.1.5)
 - подвижность дырок,
- подвижность дырок,  .
.
Электрическое поле напряженностью  действует как на электроны, так и на дырки. Так как знаки зарядов и скорости этих частиц противоположны, то соответствующие токи складываются. Поэтому в области собственной и смешанной проводимости:
действует как на электроны, так и на дырки. Так как знаки зарядов и скорости этих частиц противоположны, то соответствующие токи складываются. Поэтому в области собственной и смешанной проводимости:
 (3.1.6)
(3.1.6)
где
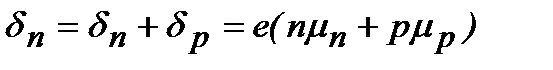 - удельная объемная проводимость материала.
- удельная объемная проводимость материала.
При наличии нескольких сортов носителей заряда с различными массами и подвижностями:
 (3.1.7)
(3.1.7)
где суммирование проводиться по всем сортам носителей.
Дрейфовый ток, обусловленный не основными носителями пренебрежимо мал по сравнению с током, который связан с основными носителями.
Еще раз заостряю внимание на следующем: в полупроводнике  - типа вектор напряженности поля и скорости электронов направлены в разные стороны, а в
- типа вектор напряженности поля и скорости электронов направлены в разные стороны, а в  - типе – одинаково направлены, т.е.
- типе – одинаково направлены, т.е.
Дата добавления: 2015-10-31; просмотров: 227 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Зависимость положения уровня Ферми от концентрации примеси и температуры. | | | Соотношение Эйнштейна |