Финансовая эквивалентность обязательств. Эквивалентность различных ставок. Вывод формул эквивалентности

При необходимости замены одного денежного обязательства другим, например с более отдаленным сроком платежа, объединении нескольких платежей в один (консолидировать платежи) возникает вопрос о принципе, на котором должны базироваться изменения условий контрактов. Таким общепринятым принципом является финансовая эквивалентность обязательств.

Эквивалентность простой ставки процентов и простой учетной ставки

Для определения эквивалентности простых ставки процентов и учетной ставки в качестве сравниваемой величины можно взять сумму процентных денег при выдаче ссуды. Сумма процентных денег при выдаче ссуды на n- лет при использовании простой ставки процентов определятся выражением

S=S0(1+in), а при использовании простой учетной ставки – выражением

S=S0/(1-dn)

Приравнивая эти выражения, получаем уравнение эквивалентности: S0(1+in)=S01/(1-dn)

1) Для нахождения простой процентной ставки через учетную:

(1+in)=1/1-dn

in=1/1-dn – 1

in=1/1-dn – 1-dn/1-dn

in=dn/1-dn

Разделив на n получаем:

Эквивалентные ставки процентов:

2) Для нахождения простой учетной ставки через простую процентную ставку:

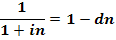
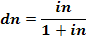
Разделив на n получаем:

Эквивалентная учетная ставка:

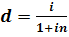
27. Формула сложных процентов. Множитель наращения и способы его определения. Дисконтирование по формуле сложных процентов. Определение срока платежа и ставки процентов. Сравнение интенсивности процессов наращения и дисконтирования по различным видам ставок.

Сложные проценты отличаются тем что доходы начисляются на не постоянную сумму, а на постоянно изменяющуюся велечину первоначальной стоимости. Изменение S0 достигается за счет капитализации процентов после каждого их начисления.

Формула наращения ставке сложных процентов:: S=S0(1+i)^n

По данной формуле можно рассчитать наращение с условием капитализации один раз в год.

Велечину (1+i)^n называют множителем наращения по сложным процентам. Множитель наращения показывает во сколько раз наращенная сумма больше первоначальной.

На практике может возникнуть задача начислением процентов и их капитализации несколько раз в год, таком случаи нужно скорректировать как ставку так и степенной коэффициенте S=S0(1+i/m)^nm где m- количество начисл % в течение года

Нами для наращения и дискантирования использовались различные ставки. Даже в одинаковых исходных условиях применение этих ставок приводит к различным результатам. В связи с этим представляет практический интерес сравнение результатов наращения и дисконтирования по различным ставкам. Для этого достаточно сопоставить соответствующие множители наращения.

Множители наращения соотносят между собой следующим образом:

(1+iсл)^n<1+niпр<1/1-nd<1/(1-d)^n при 0<n<1

1+iсл=1+iпр<1/1-dпр=1/1-d при n=1

1+niпр<(1+i)^n<1/(1-d)^n<1/1-ndпр при n>1

Соотношение множителей зависит от сроков наращения процентов. Так для срока превыщающего год наибольшии рост дает простая учетная ставка, наименьший – ставка простых процентов.

(1-d)^n<1-ndпр<1/1+ni<1/(1+i)^n при 0<n<1

1-dсл=1-dпр<1/1+iпр=1/1+i при n=1

1-ndпр<(1-d)^n<1/(1+i)^n<1/1+niпр при n>1

Для срока более года наиболее сильно дискантирование проявляется пр применении простой ставки процента и в наименьшей степени – при использовании простой учетной ставки.

28 Эквивалентность различных ставок. Вывод формул эквивалентных процентных ставок на основе уравнения эквивалентности. Финансовая эквивалентность обязательств.

Эквивалентные процентные ставки – такие ставки, значения, которых в конкретных условиях приводят к одинаковым финансовым результатам, т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых отношений сторон в рамках одной операции.

Эквивалентности ставок можно заменить для определенных операции конкретной условии на другие сохранением конечного результата наращения или дисконтирования.

Важно отметить что даже не значительных сроков проведения операции и величине одной из ставок потребует нового расчета эквивалент.

(1+niпр)=(1+iсл)^n

iпр=(1+iсл)^n-1/n

1+ iсл= n√1+ n iпр

iсл=n√1+n+iпр(корень закрывается) –1

S0процентная=S0учетная

1/1+ki = 1-kd

d=i/1+ki

прикладное значение имеет задачу выбора наиболее выгоднях условии размещения средств, для этого используются сравнение множителей (наращение или дисконтирование).

При необходимости замены одного денежного обязательства другим, например с более отдаленным сроком платежа, объединении нескольких платежей в один (консолидировать платежи) возникает вопрос о принципе, на котором должны базироваться изменения условий контрактов. Таким общепринятым принципом является финансовая эквивалентность обязательств.

Дата добавления: 2015-10-31