
Читайте также:
|
Рассмотрим модель, удовлетворяющую предпосылкам ГСБ-1 получившую название броуновского движения.
Пусть временной ряд логарифмов цены актива  в моменты времени
в моменты времени  представлен в виде дискретного процесса:
представлен в виде дискретного процесса: 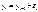 , где случайный процесс
, где случайный процесс 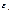 принимает в каждый момент времени
принимает в каждый момент времени  одно из двух значений:
одно из двух значений: 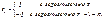 При
При  обозначим такую сумму как
обозначим такую сумму как  .На интервале
.На интервале 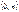 временной промежуток
временной промежуток  . Чтобы процесс
. Чтобы процесс  удовлетворял предпосылкам ГСБ-1, необходимо, чтобы его математическое ожидание и дисперсия соответствовали
удовлетворял предпосылкам ГСБ-1, необходимо, чтобы его математическое ожидание и дисперсия соответствовали  .Таким образом, имеем:
.Таким образом, имеем: 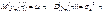 .При
.При  распределение
распределение 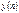 является нормальным с математическим ожиданием
является нормальным с математическим ожиданием 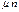 и дисперсией
и дисперсией  и для него характерны следующие свойства:
и для него характерны следующие свойства:
а) для любых  и
и 

 ;
;
б) для любых 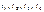
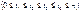
 . Процесс
. Процесс  , обладающий этими св-ми, называют арифметическим броуновским движением. В общем случае его выражение имеет вид:
, обладающий этими св-ми, называют арифметическим броуновским движением. В общем случае его выражение имеет вид:  , где
, где 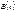 называют стандартным броуновским движением, для которого
называют стандартным броуновским движением, для которого  .
.
Дата добавления: 2015-09-05; просмотров: 88 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модели авторегрессии | | | Структурные и приведенные формы СОУ |