Читайте также:
|
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих функций. Например, нелинейными является производственная функции, функция спроса и другие.
Два класса нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам
2) регрессии, нелинейные по оцениваемым параметрам.
Для оценки параметров нелинейных моделей используются два подхода:
1) линеаризация модели (с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными)
2) нелинейная оптимизация на основе исходных переменных
Если модель нелинейна по переменным, то для оценки параметров используют обычный метод наименьших квадратов. Например, если необходимо оценить параметры регрессионной модели 
, 
, то вводя новые переменные 
, 
, получим линейную модель 
, 
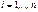, параметры которой находятся обычным методом наименьших квадратов.
К нелинейной модели по параметрам можно отнести мультипликативную модель 
, 
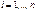, экспоненциальную модель 
, 
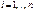. В ряде случаев эти модели удается привести к линейной форме логарифмированием обеих частей уравнения. Тогда мультипликативная модель примет вид
, , то есть вектор возмущений 
должен иметь логарифмически нормальное распределение.
Дата добавления: 2015-09-05; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интервальные прогнозные оценки значений функции регрессии в заданной точке. | | | Методы оценки коэффициентов моделей с лаговыми независимыми переменными. Метод Алмон. |