Читайте также:
|
Эконометрические модели с лаговыми независимыми переменными учитывают влияние на 
Уровней объясняющих факторов, относящихся к прошедшим моментам времени 
.
Общий вид линейной эконометрической модели с лаговыми независимыми переменными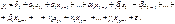 
Сформируем новый вариант эконометрической модели
. Для оценки коэффициентов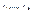 
можно использовать обычный МНК. Оценки коэффициентов 
: 
Рассм. общую модель с распредел-ым лагом, имеющую конечную максимальную величину лага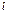 
: 
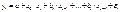. Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон.
В общем виде для полинома k-й степени имеем:
.
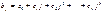Тогда 
: 
. Подставив получим:
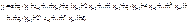
Обозначим слагаемые в скобках при 
как новые переменные:
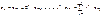
Перепишем модель: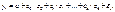 
Алгоритм метода Алмон.
1. Определяется максимальная величина лага 
.
2. Определяется степень полинома 
, описывающего структуру лага.
3. По соотношениям рассчитываются значения переменных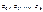 
.
4. Определяются параметры уравнения линейной регрессии.
5. С помощью соотношений рассчитываются параметры исходной модели с распределенным лагом.
Дата добавления: 2015-09-05; просмотров: 112 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нелинейные модели и линеаризация. | | | Методы оценки коэффициентов моделей с лаговыми независимыми переменными. Метод Койка. |