Читайте также:
|
Рассмотрим модель линейной регрессии, в которой регрессионные остатки 
связаны автокорреляционной зависимостью 1-го порядка, т.е. 
, где 
- некоторое число, по абсолютной величине меньшее единицы, а случайные величины 
удовлетворяют требованиям, предъявляемым к регрессионным остаткам классической модели, т.е.,
. 
,
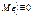представим произведение 
в виде:
.
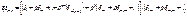получаем:
, Запишем линейную модель множественной регрессии с автокоррелированными остатками в виде:
.
Обобщенная модель сводится к классической домножением слева на матрицу преобразований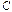 
.
21. Оценивание в модели с авторегрессией. Процедура Кохрейна – Оркатта.Значение известно. для оценки сис-мы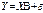 
можно применить ОМНК. Здесь 
. Для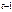 
, рассмотрим преобразование
. При 
имеем 
. Значение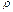 
неизвестно. Процедура Кохрейна – Оркатта. Применяем обычного МНК к исходной системе 
и получение соответствующих остатков 
. Далее: 1)в качестве приближенного значения берется его МНК-оценка 
в регрессии 
; 2) проводится преобразование при 
и находятся МНК-оценки 
; 3)строится новый вектор остатков 
;процедура повторяется, начиная с п. 1).
Процесс обычно заканчивается, когда очередное приближение мало отличается от предыдущего.
Дата добавления: 2015-09-05; просмотров: 87 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОЛММР с гетероскедастичными остатками. Взвешенный метод наименьших квадратов | | | Тест Дарбина Уотсона на автокорреляцию остатков |