Читайте также:
|
Критерий Дарбина – Уотсона основан на статистике, имеющей вид: 
,
где 
- остатки обыкновенного метода наименьших квадратов. Постоянный член включен в число регрессоров. Тогда
Предполагая, что число наблюдений достаточно большое, можно предполагать, что 
.получим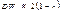 
.
Дарбин и Уотсон доказали, что сущ-ют две границы 
и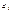 
, 
, которые обладают следующим свойством: 
"-" корреляция,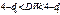 
Неопределенность, 
Нет автокорреляции, 
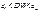Неопределенность, 
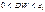"+"корреляция. Тест Дарбина – Уотсона построен в предположении, что регрессоры 
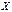и ошибки 
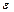не коррелированны
22. Оценивание в модели с авторегрессией. Процедура Хилдрета – Лу
Значение 
известно. В этом случае для оценки системы 
можно применить ОМНК. Здесь 
. Для 
, рассмотрим преобразование 
При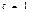 
имеем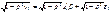 
.
Значение 
неизвестно. Процедуры оценивания при неизвестном , как правило, имеют итеративный характер.
Процедура Хилдрета – Лу. Из интервала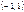 
возможного изменения коэффициента 
берутся последовательно некоторые значения и для каждого из них проводится оценивание преобразованной системы. Определяется то значение этого параметра, для которого сумма квадратов отклонений минимальна.
Дата добавления: 2015-09-05; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Автокорреляция остатков преобразования моделей | | | Точечный прогноз значения результирующего показателя в условиях ОЛММР. |