Мультиколлинеарность. Методы устранения мультиколлинеарности

Мультиколлинеарность определяется нарушением требования к рангу матрицы 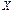- ранг мат­рицы меньше . Матрица оказывается вырожденной.

1) анализируют матрицу 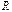парных коэффициентов корре­ляции. наличие значений коэффициентов корреляции > 0,75 - 0,80, свидетельствует о наличии мультиколлинеарности.

2) Существование тесных линейных статистических связей между объяс­няющими переменными приводит к слабой обусловленности матрицы .

3) Важную роль в анализе мультиколлинеарности играет и минимальное собственное число матрицы .

4) Мультиколлинеарность есть когда:

n некоторые из оценок имеют неправильные знаки или неоправданно большие по аб­солютной величине значения;

n небольшое изменение исходных статистических данных приво­дит к существенному изменению оценок коэффициентов мо­дели, вплоть до изменения их знаков;

n большинство или даже все оценки коэффициентов регрессии ока­зываются статистически незначимо отличающимися от нуля, а модель в целом является значимой при проверке с помощью статистики .

Методы устранения мультиколлинеарности

1. Переход к смещённым методам оценивания. Подходом называемый “ ридж - регрессией”. Он основан на рас­смотрении однопараметрического семейства “подправленных” МНК - оценок:

.

2. Переход к ортогонализированным объясняющим переменным с по­мощью метода главных компонент.

3. Отбор наиболее существенных объясняющих переменных.

16. Тесты на гетероскедастичность. Тест Голдфелда – Куандта(Goldfeld – Quandt).

В тесте проверяется основная гипотеза против альтернатив­ной гипотезы .

Этот тест применя­ется когда есть предположение о прямой зависимости дисперсии ошибки от величины некоторой независимой переменной. Тест проводится следующим образом:

1) упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность; исключить средних наблюдений;

2) провести две независимые регрессии первых наблюдений и последних 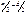наблюдений и построить соответствующие остатки и ;

3) составить статистику . Если верна гипотеза , то имеет распределение Фишера с 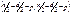степенями свободы. Большая величина этой статистики означает, что гипотезу следуетотвергнуть.

17. Тесты на гетероскедастичность. Тест Бреуша – Пагана (Breusch – Pagan).

В тесте проверяется основная гипотеза против альтернатив­ной гипотезы . Этот тест применяется в тех случаях, когда априорно предполагается, что дисперсии зависят от некоторых дополнительных переменных: , , где - вектор независимых переменных, 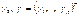- неизвестные параметры. Тест Бреуша – Пагана предполагает выполнение следующих действий:

1) провести обычную регрессию и получить вектор остатков ;

2) построить оценку ;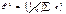

3) провести регрессию и найти для нее объясненную часть вариации ;

4) построить статистику . Установлено, что если верна гипотеза , то величина асимптотически имеет распределение .

При выявлении гетероскедастичности можно попытаться коррекцию с помощью метода взвешенных наименьших квадратов, выбирая в качестве весов величины , где - оценки.

Процедура теста Бреуша – Пагана выглядит тогда совершенно аналогично с заменой регрессии на регрессию .

Дата добавления: 2015-09-05