Читайте также:
|
Пусть мы располагаем исходными статистическими данными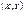 
, статистическая связь между 
и 
может быть описана регрессионной моделью ОЛММР. Известна оценена ковариационная матрица регрессионных остатков 
. Заданы значения объясняющих переменных 
, но значение результирующего показателя 
нам неизвестно. 
, 
и 
. Требуется построить наилучший линейный и несмещенный прогноз для 
.
Нам необходимо найти 
, который бы обладал свойством: 
,
должны удовлетворять условию: 
.
Обозначим 
Проанализируем средний квадрат ошибки прогноза:
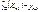
,следует: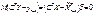 
,
т.е. вектор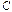 
должен удовлетворять условию 
.Поэтому: 
.
Далее, минимизируем полученное выражение при условии 
по 
. 
для оптимального прогноза:
.
Таким образом, наилучшим линейным несмещенным прогнозом значения 
будет 
.
Дата добавления: 2015-09-05; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тест Дарбина Уотсона на автокорреляцию остатков | | | Оценивание в модели с авторегрессией. Процедура Дарбина |