Читайте также:
|
Требуется при заданной величине доверительной вероятности 
построить основанный на наилучшем линейном несмещенном точечном прогнозе 
интервальный прогноз для значения результирующего показателя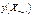 
. Средний квадрат ошибки оптимального прогноза 
.
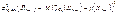Поскольку точечный прогноз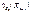 
по построению является линейной функцией от 
, а последние в силу нормального распределения остатков сами подчиняются нормальному закону, то и разность 
является нормально распределенной случайной величиной со средним значением, равным нулю и с дисперсией 
. Следовательно, границы искомого интервального прогноза определяются по формулам:
В случае классической линейной модели можно получить формулу в виде:
,
где 
- оценки коэффициентов парной регрессии обычным методом наименьших квадратов, 
- заданное значение объясняющей переменной, а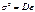 
- дисперсия регрессионных остатков в классической модели линейной регрессии.
Дата добавления: 2015-09-05; просмотров: 97 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оценивание в модели с авторегрессией. Процедура Дарбина | | | Интервальные прогнозные оценки значений функции регрессии в заданной точке. |