|
Читайте также: |
Выведем формулу для интервального прогноза неизвестного значения линейной регрессии 
при заданном значении 
в условиях ОЛММР. Вычислим средний квадрат ошибки точечного прогноза:
Наилучшая линейная несмещенная точечная оценка 
неизвестного значения функции регрессии 
- это нормально распределенная случайная со средним значением равным 
и с дисперсией 
. Поэтому неизвестное значение функции регрессии 
с вероятностью 
должно принадлежать интервалу
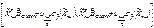. Для класс-ой модели парной регрессии 
:
.
Дата добавления: 2015-09-05; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интервальный прогноз значения результирующего показателя в условиях нормальной ОЛММР. | | | Нелинейные модели и линеаризация. |