Читайте также:
|
Тестирование математического ожидания
Интервал времени 
разбивается на две части. Для каждой из частей определяются оценки 
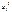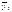и 
, 
и 
. Далее рассчитывается значение критерия Стьюдента: если 
,то 
если 
, то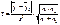 
. Если 
, то гипотезу о постоянстве математического ожидания целесообразно принять. При 
, эта гипотеза отвергается.
Также используется критерий Фишера: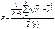 
, где 
- число частей разбиения интервала 
; 
- число измерений переменной 
на 
-й части; 
; 
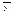- среднее значение временного ряда в целом; 
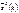- средняя дисперсия: 
, где 
- дисперсия, рассчитанная на 
-й части интервала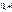 
. Если 
, то гипотеза о постоянстве матем-кого ожидания временного ряда принимается.
Тестирование дисперсии
значение критерия Фишера определяется: 
, где 
и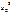 
- оценки дисперсии ряда на 1 и 2 частях соответственно с числом измерени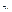й 
и 
.
Если значение 
удовлетворяет неравенству 
, то гипотеза о постоянстве дисперсии временного ряда может быть принята.
При больших выборках расчетное значение стандартизованной случайной величины оценивается как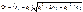 
.
если 
, где 
- табличное значение стандартизованного нормального закона, то гипотеза о постоянстве дисперсии принимается.
Тестирование коэффициентов автокорреляции
Теоретически для проверки гипотезы о постоянстве коэффициентов автокорреляции могут использоваться те же процедуры, что и для проверки аналогичных гипотез для средних (автокорреляция) и дисперсии (автоковариация). При использовании критерия Стьюдента дисперсия выборочных коэффициентов автокорреляции определяются с достаточно большой погрешностью, которая увеличивается с ростом значений самого коэффициента автокорреляции.
Дата добавления: 2015-09-05; просмотров: 123 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Стационарные временные ряды. Тесты стационарности | | | Временные ряды. Десезонализация ряда методом фиктивных переменных. Аддитивная модель. |