Читайте также:
|
Общий вид линейной эконометрической модели с лаговыми зависимыми переменными может быть выражен следующим уравнением: 
,
где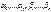 
- коэф-ты модели; 
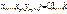- переменные модели, 
- ошибка. Необходимость включения в правую часть модели лаговых зависимых переменных часто определяется специфическими свойствами исследуемого объекта, например, его инерционностью.
Проблемы оценки параметров модели, обусловленные плохой обратимостью матрицы 
, для этого обратимся к модели с лаговыми независимыми переменными, рассмотренной Койком. Модель Койка представим в виде следующего уравнения:
. Используя оператор сдвига 
: 
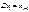. Тогда 
, где 
- общий множитель коэффициентов. 
находятся в зависимости, соответствующей убывающей геометрической прогрессии. Тогда можно записать: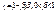 
. В этом случае: 
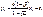, где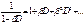 
. Используя свойства оператора сдвига: 
. Ошибка модели 
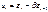коррелирует с лаговой переменной 
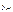, поскольку 
и 
корреляционно взаимосвязаны.
Дата добавления: 2015-09-05; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методы оценки коэффициентов моделей с лаговыми независимыми переменными. Метод Койка. | | | Стационарные временные ряды. Тесты стационарности |