Читайте также:
|
Общий вид модели авторегрессии k-го порядка – АР(k) задается уравнением: 
, где 
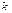- порядок модели, 
- случайная ошибка с нулевым матем-им ожиданием.
Построение модели АР(k) предполагает решение двух взаимосвязанных задач: определение рационального порядка модели и оценки значений ее коэффициентов. 
. Умножим выражение на 
и возьмем математическое ожидание, получим: 
, где 
представляет собой ковариацию 
на практике оцениваемую по формуле
.
Предполагая, что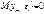 
, получим 
. Разделив обе части уравнения на дисперсию процесса 
, получим: 
. Подставив вместо 
процесса 
их выборочные оценки 
, получим следующую систему уравнений:
Положим если 
, тогда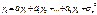 
, где 
- i-й коэф. автоковариации. Т.к. 
, получим 
. Модель авторегрессии считается «достаточно хорошей», если 
.
Дата добавления: 2015-09-05; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Преобразования нестационарных временных рядов в стационарные | | | Модели ГСБ-1. Броуновское движение. |